2022 CryptoCTF

Van1sh 比赛小屋
创建时间:
字数:16.8k 阅读:
  1. warm-up
    1. Mic-Check
  2. easy
    1. Klamkin
      1. challenge
      2. thought
      3. exp
      4. result
    2. Baphomet
      1. challenge
      2. thought
      3. exp
      4. result
  3. medium-easy
    1. SOTS
      1. challenge
      2. Thought
      3. exp
      4. result
    2. polyRSA
      1. challenge
      2. Thought
      3. exp
      4. result
    3. Infinity castle
      1. challenge
      2. Thought
      3. exp
      4. result
    4. Keydream
      1. challenge
      2. Thought
      3. exp
      4. result
    5. Jeksign
      1. challenge
      2. Thought
      3. exp
      4. result
    6. Volgo
      1. challenge
      2. Thought
      3. exp
      4. result
  4. medium
    1. Aniely
      1. challenge
      2. Thought
      3. exp
      4. result
    2. Diploma
      1. challenge
      2. Thought
      3. exp
      4. result
    3. Oak land
      1. challenge
      2. Thought
      3. exp
      4. result
    4. Cantilever
      1. challenge
      2. Thought
      3. exp
      4. result
    5. Side step
      1. challenge
      2. Thought
      3. exp
      4. result
    6. Faonsa *
      1. challenge
      2. Thought
      3. exp
      4. result
    7. Resign
      1. challenge
      2. Thought
      3. exp
      4. result
    8. DBB
      1. challenge
      2. Thought
      3. exp
      4. result
    9. Fiercest
      1. challenge
      2. Thought
      3. exp
      4. result
    10. Mino *
      1. challenge
      2. Thought
      3. exp
      4. result
    11. Starter ECC
      1. challenge
      2. Thought
      3. exp
      4. result
  5. medium-hard
    1. Watery soup
      1. challenge
      2. Thought
      3. exp
      4. result
    2. 313 Loyal
      1. challenge
      2. Thought
      3. exp
      4. result
    3. Soda*
      1. challenge
      2. Thought
      3. exp
      4. result
    4. Sparse*
      1. challenge
      2. Thought
      3. exp
      4. result
    5. Larisa
      1. challenge
      2. Thought
      3. exp
      4. result
    6. Shaim
      1. challenge
      2. Thought
      3. exp
      4. result
    7. Lagima
      1. challenge
      2. Thought
      3. exp
      4. result
    8. Versace
      1. challenge
      2. Thought
      3. exp
      4. result
  6. hard
    1. GSDP
      1. challenge
      2. Thought
      3. exp
      4. result
    2. Persian cat
      1. challenge
      2. Thought
      3. exp
    3. NLCS x
      1. challenge

warm-up

Mic-Check

分值：19

考点：签到

Can you hear me?2022-Jul-Thu 12:20:26

If you can, enter your first flag:

1
CCTF{Th3_B3sT_1S_Yet_t0_C0m3!!}

easy

Klamkin

分值：61

考点：Congruence

challenge

We need to have a correct solution!

1
nc 04.cr.yp.toc.tf 13777
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
[root@VM-0-7-centos ~]# nc 04.cr.yp.toc.tf 13777
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  Hello, now we are finding the integer solution of two divisibility  |
|  relation. In each stage send the requested solution. Have fun :)    |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We know (ax + by) % q = 0 for any (a, b) such that (ar + bs) % q = 0
| and (q, r, s) are given!
| Options: 
|	[G]et the parameters 
|	[S]end solution 
|	[Q]uit
G
| q = 289932383341902531151841340632555887679
| r = 197196838427345567639010598439485580615
| s = 59132640739541526585077026866726580617
| Options: 
|	[G]et the parameters 
|	[S]end solution 
|	[Q]uit
S
| please send requested solution like x, y such that y is 12-bit:

thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import *
from pwn import *


def x(n):
    x = getPrime(n)
    y = -a*x*inverse(b,q) % q
    assert (a*x + b*y) % q == 0
    sh.sendline(str(x)+","+str(y))


def y(n):
    y = getPrime(n)
    x = -b*y*inverse(a,q) % q
    assert (a*x + b*y) % q == 0
    sh.sendline(str(x)+","+str(y))


sh = remote("04.cr.yp.toc.tf",13777)
context.log_level = 'debug'

sh.recvuntil("[Q]uit")
sh.sendline("G")

sh.recvuntil("| q = ")
q = int(sh.recvuntil("\n")[:-1])
sh.recvuntil("| r = ")
r = int(sh.recvuntil("\n")[:-1])
sh.recvuntil("| s = ")
s = int(sh.recvuntil("\n")[:-1])

sh.recvuntil("[Q]uit")
sh.sendline("S")

while True:
    a = inverse(r,q)
    b = inverse(-s,q)
    assert (a*r + b*s) % q == 0

    ch = sh.recvuntil("bit: \n").split(b" ")
    print(ch)
    if ch[-4]== b"x":
        x(int(ch[-2][:2]))
    else:
        y(int(ch[-2][:2]))

sh.interactive()

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
[+] Opening connection to 04.cr.yp.toc.tf on port 13777: Done
[DEBUG] Received 0xdb bytes:
    b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n'
    b'|  Hello, now we are finding the integer solution of two divisibility  |\n'
    b'|  relation. In each stage send the requested solution. Have fun :)    |\n'
[DEBUG] Received 0xeb bytes:
    b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n'
    b'| We know (ax + by) % q = 0 for any (a, b) such that (ar + bs) % q = 0\n'
    b'| and (q, r, s) are given!\n'
    b'| Options: \n'
    b'|\t[G]et the parameters \n'
    b'|\t[S]end solution \n'
    b'|\t[Q]uit\n'
[DEBUG] Sent 0x2 bytes:
    b'G\n'
[DEBUG] Received 0xc7 bytes:
    b'| q = 248930089074638341399935646008896010497\n'
    b'| r = 65697821096685931683761068135861058583\n'
    b'| s = 8664059547396611157411147813907067755\n'
    b'| Options: \n'
    b'|\t[G]et the parameters \n'
    b'|\t[S]end solution \n'
    b'|\t[Q]uit\n'
[DEBUG] Sent 0x2 bytes:
    b'S\n'
[DEBUG] Received 0x43 bytes:
    b'| please send requested solution like x, y such that y is 12-bit: \n'
[b'\n|', b'please', b'send', b'requested', b'solution', b'like', b'x,', b'y', b'such', b'that', b'y', b'is', b'12-bit:', b'\n']
[DEBUG] Sent 0x2c bytes:
    b'36385751892032159627624237030492875755,3539\n'
[DEBUG] Received 0x72 bytes:
    b'| good job, try to solve the next challenge :P\n'
    b'| please send requested solution like x, y such that y is 13-bit: \n'
[b'|', b'good', b'job,', b'try', b'to', b'solve', b'the', b'next', b'challenge', b':P\n|', b'please', b'send', b'requested', b'solution', b'like', b'x,', b'y', b'such', b'that', b'y', b'is', b'13-bit:', b'\n']
[DEBUG] Sent 0x2d bytes:
    b'134300229126114739440789160858242865128,7993\n'
[DEBUG] Received 0x72 bytes:
    b'| good job, try to solve the next challenge :P\n'
    b'| please send requested solution like x, y such that y is 16-bit: \n'
[b'|', b'good', b'job,', b'try', b'to', b'solve', b'the', b'next', b'challenge', b':P\n|', b'please', b'send', b'requested', b'solution', b'like', b'x,', b'y', b'such', b'that', b'y', b'is', b'16-bit:', b'\n']
[DEBUG] Sent 0x2e bytes:
    b'196535357683169499069413298376157574596,49991\n'
[DEBUG] Received 0x72 bytes:
    b'| good job, try to solve the next challenge :P\n'
    b'| please send requested solution like x, y such that x is 16-bit: \n'
[b'|', b'good', b'job,', b'try', b'to', b'solve', b'the', b'next', b'challenge', b':P\n|', b'please', b'send', b'requested', b'solution', b'like', b'x,', b'y', b'such', b'that', b'x', b'is', b'16-bit:', b'\n']
[DEBUG] Sent 0x2e bytes:
    b'36847,229436344314746801153667328942317085633\n'
[DEBUG] Received 0x72 bytes:
    b'| good job, try to solve the next challenge :P\n'
    b'| please send requested solution like x, y such that y is 19-bit: \n'
[b'|', b'good', b'job,', b'try', b'to', b'solve', b'the', b'next', b'challenge', b':P\n|', b'please', b'send', b'requested', b'solution', b'like', b'x,', b'y', b'such', b'that', b'y', b'is', b'19-bit:', b'\n']
[DEBUG] Sent 0x2e bytes:
    b'90733961161770834421760416122416141408,462541\n'
[DEBUG] Received 0x4e bytes:
    b'| Congrats, you got the flag: CCTF{f1nDin9_In7Eg3R_50Lut1Ons_iZ_in73rEStIn9!}\n'

Baphomet

分值：56

考点：已知明文攻击

challenge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#!/usr/bin/env python3

from base64 import b64encode
from flag import flag

def encrypt(msg):
	ba = b64encode(msg.encode('utf-8'))
	baph, key = '', ''

	for b in ba.decode('utf-8'):
		if b.islower():
			baph += b.upper()
			key += '0'
		else:
			baph += b.lower()
			key += '1'

	baph = baph.encode('utf-8')
	key = int(key, 2).to_bytes(len(key) // 8, 'big')

	enc = b''
	for i in range(len(baph)):
		enc += (baph[i] ^ key[i % len(key)]).to_bytes(1, 'big')

	return enc

enc = encrypt(flag)
f = open('flag.enc', 'wb')
f.write(enc)
f.close()

thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#!/usr/bin/env python3
#
with open("flag.enc","rb") as f:
	enc = f.read()
print(len(enc))

from base64 import b64encode,b64decode
msg=b"CCTF{"
ba = b64encode(msg)
baph, key = '', ''
for b in ba.decode('utf-8'):
	if b.islower():
		baph += b.upper()
		key += '0'
	else:
		baph += b.lower()
		key += '1'

baph = baph.encode('utf-8')[:6]
print(baph)

key = b""
for i in range(len(baph)):
	key += (baph[i] ^ enc[i]).to_bytes(1, 'big')
print(key)

dec = b""
for i in range(len(enc)):
	dec += (enc[i] ^ key[i % len(key)]).to_bytes(1, 'big')
print(dec)

flag=""
for b in dec.decode('utf-8'):
	if b.islower():
		flag += b.upper()
	else:
		flag += b.lower()
print(b64decode(flag.encode('utf-8')))
#key = int(key, 2).to_bytes(len(key) // 8, 'big')

result

1
2
3
4
5
6
48
b'q0nurN'
b'\xf9b\xad\xacN\xff'
b'q0nurNTvCfaZCL8WuL9St3DfuL8Xn1PFDeGZx1bYmgjmm019'
b'CCTF{UpP3r_0R_lOwER_17Z_tH3_Pr0bL3M}'
[Finished in 0.2s]

medium-easy

SOTS

分值：49

考点：two_square

challenge

He who abides far away from his home, is ever longing for the day he shall return.

1
nc 05.cr.yp.toc.tf 37331
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
[root@VM-0-7-centos ~]# nc 05.cr.yp.toc.tf 37331
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  Hey math experts, in this challenge we will deal with the numbers   |
|  those are the sum of two perfect square, now try hard to find them! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Generating the `n', please wait...
| Options: 
|	[G]et the n 
|	[S]olve the challenge! 
|	[Q]uit
G
| n = 1243565868390316746681363697659435925395524656187056587629633961874200469
| Options: 
|	[G]et the n 
|	[S]olve the challenge! 
|	[Q]uit
S
| Send your pair x, y here:

Thought

exp

https://www.alpertron.com.ar/QUAD.HTM

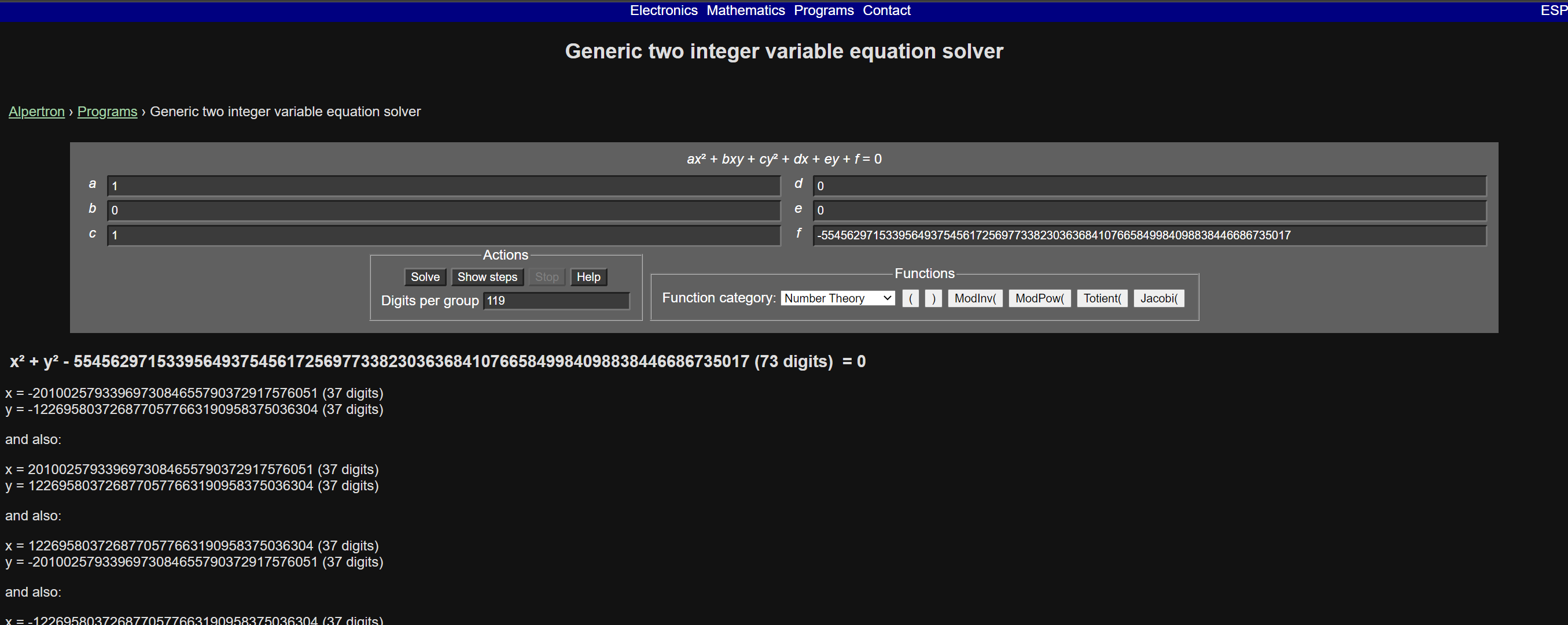
image-20220718153538221

1
2
3
4
# sagemath

sage: two_squares(5545629715339564937545617256977338230363684107665849984098838446686735017)
(1166738044093249132248421369078945211, 2045568882195127737861825295828693636)

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
root@VM-0-7-centos ~]# nc 05.cr.yp.toc.tf 37331
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  Hey math experts, in this challenge we will deal with the numbers   |
|  those are the sum of two perfect square, now try hard to find them! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Generating the `n', please wait...
| Options: 
|	[G]et the n 
|	[S]olve the challenge! 
|	[Q]uit
g
| n = 5545629715339564937545617256977338230363684107665849984098838446686735017
| Options: 
|	[G]et the n 
|	[S]olve the challenge! 
|	[Q]uit
s
| Send your pair x, y here: 
2010025793396973084655790372917576051,1226958037268770577663190958375036304
| Congratz! the flag is CCTF{3Xpr3sS_4z_Th3_sUm_oF_7w0_Squ4rE5!}

polyRSA

分值：42

考点：RSA

challenge

Hello RSA, my old friend!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

def keygen(nbit = 64):
	while True:
		k = getRandomNBitInteger(nbit)
		p = k**6 + 7*k**4 - 40*k**3 + 12*k**2 - 114*k + 31377
		q = k**5 - 8*k**4 + 19*k**3 - 313*k**2 - 14*k + 14011
		if isPrime(p) and isPrime(q):
			return p, q

def encrypt(msg, n, e = 31337):
	m = bytes_to_long(msg)
	return pow(m, e, n)

p, q = keygen()
n = p * q
enc = encrypt(flag, n)
print(f'n = {n}')
print(f'enc = {enc}')

Thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n = 44538727182858207226040251762322467288176239968967952269350336889655421753182750730773886813281253762528207970314694060562016861614492626112150259048393048617529867598499261392152098087985858905944606287003243
enc = 37578889436345667053409195986387874079577521081198523844555524501835825138236698001996990844798291201187483119265306641889824719989940722147655181198458261772053545832559971159703922610578530282146835945192532
R.<k> = ZZ[]

p = k**6 + 7*k**4 - 40*k**3 + 12*k**2 - 114*k + 31377
q = k**5 - 8*k**4 + 19*k**3 - 313*k**2 - 14*k + 14011

f = p*q-n
x = f.roots()[0][0]

pp=p(x)
qq=q(x)
phi = (pp-1)*(qq-1)
d = inverse_mod(31337,phi)
from Crypto.Util.number import *
print(long_to_bytes(pow(enc,d,n)))

result

1
b'CCTF{F4C70r!N9_tRIcK5_aR3_fUN_iN_RSA?!!!}'

Infinity castle

分值：131

考点：二次方、三次方、立方和、平方差、积分、泰勒展开

challenge

Can you break our new schema and decrypt the mixed encrypted message without having the public key and shared secret?!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#!/usr/bin/env python3

from Crypto.Util.number import *
from os import urandom

class TaylorSeries():

	def __init__(self, order):
		self.order = order
		
	def coefficient(self, n):
		i = 0
		coef = 1
		while i < n:
			i += 1
			coef *= (coef * (1/2-i+1)) / i
		return coef

	def find(self, center):
		sum = 0
		center -= 1
		i = 0
		while i < self.order:
			sum += (center**(1/2-i) * self.coefficient(i))
			i += 1
		return sum

def xor(cip, key):
	repeation = 1 + (len(cip) // len(key))
	key = key * repeation
	key = key[:len(cip)]
	
	msg = bytes([c ^ k for c, k in zip(cip, key)])
	return msg

# If you run these 3 functions (diamond, triage, summarize) with big numbers, they will never end
# You need to optimize them first

def diamond(num):
	output = 0
	for i in range(num):
		output += i*2 + 1
	return output

def triage(num):
	output = 0
	index = 0
	for i in range(num):
		output += (i+index)*6 + 1
		index += i
	return output

def summarize(b):
	order = getRandomRange(1000, 2000)
	t = TaylorSeries(order)
	output = 0
	
	i = 2
	while i < b:
		b1 = t.find(i)
		b2 = t.find(i+1)
		output += (b1+b2) / 2
		i += 1
	return output

KEY_SIZE = 2048
p, q = [getPrime(KEY_SIZE) for _ in '01']

e, n = 0x10001, p*q

f = open ('./message.txt', 'rb')
message = f.read()
f.close()
msg_length = len(message)
padded_msg = message + urandom(len(long_to_bytes(n)) - msg_length)
padded_msg_length = len(padded_msg)

xor_key = long_to_bytes(int(summarize(n)))[:padded_msg_length]
assert(len(xor_key) == 512)

enc0 = xor(padded_msg, xor_key)
assert(bytes_to_long(enc0) < n)

c0 =  abs(diamond(p) - diamond(q))
c1 =  triage(p)
c1 += 3*n*(p+q)
c1 += triage(q)

m = bytes_to_long(enc0)
enc1 = pow(m, e, n)

print(f"c0 = {c0}")
print(f"c1 = {c1}")
print(f"enc = {enc1}")

Thought

diamond：$n^2$

triage：$n^3$

summarize：$\int_\infin \sqrt{n}=\frac{2}{3}n^{\frac{3}{2}}$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def xor(cip, key):
	repeation = 1 + (len(cip) // len(key))
	key = key * repeation
	key = key[:len(cip)]
	msg = bytes([c ^^ k for c, k in zip(cip, key)])
	return msg

c0 = 194487778980461745865921475300460852453586088781074246328543689440168930873549359227127363759885970436167330043371627413542337857082400024590112412164095470165662281502211335756288082198009158469871465280749846525326701136380764079685636158337203211609233704905784093776008350120607841177268965738426317288541638374141671346404729428158104872411498098187946543666987926130124245185069569476433120128275581891425551325847219504501925282012199947834686225770246801353666030075146469275695499044424390475398423700504158154044180028733800154044746648133536737830623670383925046006108348861714435567006327619892239876863209887013290251890513192375749866675256952802329688897844132157098061758362137357387787072005860610663777569670198971946904157425377235056152628515775755249828721767845990597859165193162537676147173896835503209596955703313430433124688537275895468076469102220355973904702901083642275544954262724054693167603475188412046722656788470695566949847884250306735314144182029335732280420629131990311054229665691517003924788583771265625694414774865289407885678238795596912006567817508035434074250123869676396153982762032750080222602796273083162627489526255501643913672882350236497429678928099868244687228703074267962827621792960
c1 = 102325064080381160170299055162846304227217463467232681115953623386548494169967745781550171804781503102663445039561476870208178139548389771866145006535051362059443515034504958703659546162037904784821960707630188600064568878674788077706711506213779443920430038560373854184526850365974450688458342413544179732143225845085164110594063440979455274250021370090572731855665413325275414458572412561502408983107820534723804225765540316307539962199024757378469001612921489902325166003841336027940632451584642359132723894801946906069322200784708303615779699081247051006259449466759863245508473429631466831174013498995506423210088549372249221415401309493511477847517923201080509933268996867995533386571564898914042844521373220497356837599443280354679778455765441375957556266205953496871475611269965949025704864246188576674107448587696941054123618319505271195780178776338475090463487960063464172195337956577785477587755181298859587398321270677790915227557908728226236404532915215698698185501562405374498053670694387354757252731874312411228777004316623425843477845333936913444143768519959591070492639650368662529749434618783626718975406802741753688956961837855306815380844030665696781685152837849982159679122660714556706669865596780528277684800454866433826417980212164051043504955615794706595412705883261111953152250227679858538249797999044336210905975316421254442221408945203647754303635775048438188044803368249944201671941949138202928389951227347433255867504906597772044398973241425387514239164853656233776024571606159378910745571588836981735827902305330330946219857271646498602227088657739442867033212012876837654750348578740516798444734534291467314881324902354425889448102902750077077381896216130734894767553834949561471219923459897244690006643798812989271282475503126962274052192342840870308710338336817452628324667507548265612892611100350882163205858101959976
enc = 122235247669762131006183252122503937958296387791525458429403709404875223067116491817728568224832483391622109986550732469556761300197133827976956875865159629512476600711420561872409721582387803219651736262581445978042694384374119142613277808898398213602093802571586386354257378956087240174787723503606671543195193114158641301908622673736098768829071270132073818245595918660134745516367731595853832524328488074054536278197115937409643221809577554866060292157239061557708159310445977052686561229611117673473208278176118561352693319461471419694590218295911647368543698198762827636021268989705079848502749837879584394379300566277359149621932579222865430374652678738198451655509408564586496375811666876030847654260305392984710580761255795785508407844683687773983669843744274915862335181251050775093896006210092665809300090715190088851654138383362259256212093670748527819287681468901379286722214112321906917311154811516336259463356911326393701445497605365038857575515541024824906818473933597129846235905072394148879079996812146836910199111439031562946495046766063326815863624262541346543552652673629442370320109404700346028639853707278295255350982238521659924641921142615894039995513480511108116053798143154593343124822462519555715118822045

var('p,q')

f1 = p^2-q^2 - c0
f2 = (p+q)^3 - c1

#solve([f1,f2],p,q)
p=25465500595039564722385454268618341460440964303654692306893194812608651011894765148023201769023925823267446913594798724374078776058926548056279105656348138942211069695157129067986030357247987537066065195208337853580939616954961742954173270603234042184081995050125067398704045490448077961447418406856674045777724275017678698252609741079175784928310951915104807404003531834525200421059550762294584722178356010146438598799668537922242765662363844939035164178525445220653839693135494967926642943210917823981779895464411806829004306900926935124663285407830585204630912848783431051369106939431567473170247979142455819150893
q=21307368246113800130311098641506744510559988209047095448061577734947715969121645982743962584143752085867914325394457857827478912559095766977509129246922499990951138184298921892924074303356650532229644986118338361761354192554363128824141104808606558539422865199413633150757655174985683830034245659632460363700309887626934298289805670092066041542014924213128271705967504359900458092855272034197878632989626323553684162988741101770565319360726673172671459797955787997515498457867020749156835947018833861229200382521269341946614058721285386773372009177934062994798868703374266787876752211055631019633581263575312198649933
phi=(p-1)*(q-1)
e=0x10001
from Crypto.Util.number import *
d=inverse(e,phi)
n = p*q
padded_msg = long_to_bytes(pow(enc,d,n))

xor_key = long_to_bytes(int(2/3*n^(3/2)))[:512]
enc0 = xor(padded_msg, xor_key)
print(enc0)

result

1
b'Never heard of using taylor series and integral beside RSA?!\nBut there are always ways to make things complicated\n\nCCTF{Mix1ng_c4lcUluS_w17h_Numb3r_The0Rry_S33ms_s7r0ng_cRyp70_Sch3m4!!}\n\nWe compute integrals with just measuring the area with a little fraction, forget about tough works!\nGood luck with the rest of CryptoCTF2022\x9a\x92W\xcf\xa2dl\x1a\x91\x96\'\x88\xec\xfez\xcd\xc2\xe7\x0bC\x90\xa3\xc7\xe7U\xb4F\xa535V\x19\x9b\x9e\xd4\xf7\xe7X\x02\x19Y\x86\xfa\x9f\x0b!\x9a\xc1\xd2\xcayG\x8af/\x14\xef\xf9\x1d\xc2\x9a\xcb\x9da}g8\xb8\\ 2~\xf3\xe3\xb6$\xb6i\x12\xd6\x82\xfac\x15\xeeVa[s\xa0S\x00y\x0c\x18\xc34\xbd\x96fd\xec\xcf\xb9\x02<Q\x8b\xb8\x9d\xd5\xefDu\xda\xd2\xf0\xc6g\x97\xf8\x952\x0c\rs=\x19.\x11"\x08\x81\xe7*\x87\xb8\xbd>\x82\n~\xf7l,\tu\x96}*\xab`\x17\xe7\xf4\xd7N^\xe3\xfe\xf3@\x1e\x1c\x15\xffC\xecVVr\xca\x8d\x03\xc5\xda\xd6\xbf=\xc6\x14+\xf2\x14N'

Keydream

分值：105

考点：RSA

challenge

Everything is better homemade, we developed a homemade RSA, test it to see if it’s really better?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#!/usr/bin/env python3

from Crypto.Util.number import *
import string
from flag import flag

def randstr(l):
	rstr = [(string.printable[:62] + '_')[getRandomRange(0, 62)] for _ in range(l)]
	return ''.join(rstr)


def encrypt(msg, l):
	while True:
		rstr = 'CCTF{it_is_fake_flag_' + randstr(l) + '_90OD_luCk___!!}'
		p = bytes_to_long(rstr.encode('utf-8'))
		q = bytes_to_long(rstr[::-1].encode('utf-8'))
		if isPrime(p) and isPrime(q):
			n = p * q
			e, m = 65537, bytes_to_long(msg.encode('utf-8'))
			c = pow(m, e, n)
			return n, c

n, c = encrypt(flag, 27)

print(f'n = {n}')
print(f'c = {c}')

Thought

$f = phigh\cdot 2^x+unknow \cdot 2^y+plow$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n = 23087202318856030774680571525957068827041569782431397956837104908189620961469336659300387982516148407611623358654041246574100274275974799587138270853364165853708786079644741407579091918180874935364024818882648063256767259283714592098555858095373381673229188828791636142379379969143042636324982275996627729079
c = 3621516728616736303019716820373078604485184090642291670706733720518953475684497936351864366709813094154736213978864841551795776449242009307288704109630747654430068522939150168228783644831299534766861590666590062361030323441362406214182358585821009335369275098938212859113101297279381840308568293108965668609

from Crypto.Util.number import *

phigh = bytes_to_long(b"CCTF{it_is_fake_flag_")
plow = bytes_to_long(b'_90OD_luCk___!!}')
P.<x> = PolynomialRing(Zmod(n))
f = (phigh << 344) + (x * 2^128) + plow
x0 = f.monic().small_roots(X=2^216, beta=0.4,epsilon=0.02)[0]
p = int(f(x0))
q = n//p
e = 65537
phi = (p-1)*(q-1)
d = inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))

result

1
'Congratz, the flag is: CCTF{h0M3_m4dE_k3Y_Dr1vEn_CrYp7O_5ySTeM!}'

Jeksign

分值：100

考点：丢番图方程

challenge

Solve the equation, we like to have the solution!

1
nc 02.cr.yp.toc.tf 17113
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#!/usr/bin/env python3

from Crypto.Util.number import *
from secret import gensol, nbit_gensol
from flag import flag

m = bytes_to_long(flag.encode('utf-8'))
print(m)

a = 1337
b = 31337

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Welcome crypto guys! Here we are looking for the solution of special", border)
	pr(border, "Diophantine equation: 1337(z^4 - x^2) = 31337(y^2 - z^4) in natural ", border)
	pr(border, "numbers, in each stage solve the equation in mentioned interval :)  ", border)
	pr(border*72)

	STEP, level = 0, 19

	while True:
		p, q = nbit_gensol(1337, 31337, STEP + 30)
		x, y, z = gensol(a, b, p, q)
		pr(border, f"Send a solution like `x, y, z' such that the `z' is {STEP + 30}-bit: ")
		ans = sc()
		try:
			X, Y, Z = [int(_) for _ in ans.split(',')]
			NBIT = Z.bit_length()
		except:
			die(border, 'Your input is not valid, Bye!')
		if 1337*(Z**4 - X**2) == 31337*(Y**2 - Z**4) and NBIT == STEP + 30:
			if STEP == level - 1:
				die(border, f'Congrats, you got the flag: {flag}')
			else:
				pr('| good job, try to solve the next challenge :P')
				STEP += 1
		else:
			die(border, 'your answer is not correct, Bye!!')

if __name__ == '__main__':
	main()

Thought

$1337(z^4-x2)=31337(y^2-z^4)$

$(1337+31337)z^4=1337x^2+31337y^2$

$x=y=z^2$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
from Crypto.Util.number import *
from sympy import *

from pwn import *
context.log_level = 'debug'
sh = remote("02.cr.yp.toc.tf",17113)
for i in range(30,49):
	ch = sh.recvuntil("-bit: \n")
	z = getPrime(i)
	x = z**2
	y = x
	sh.sendline(str(x)+","+str(y)+","+str(z))
sh.interactive()

result

1
| Congrats, you got the flag: CCTF{4_diOpH4nT1nE_3Qua7i0n__8Y__Jekuthiel_Ginsbur!!}

Volgo

分值：

考点：

challenge

There is no land behind the Volga!! The Soviets surround us,and we have only a single key table to communicate to the outside!! Hopefully, the Soviets wouldn’t be able read our messages.

1
http://03.cr.yp.toc.tf:11117/

image-20220719094430434

GET ENCRYPTDE FLAG :)

1
2
3
4
5
6
7
{"flag": "ZZNVH EOOAA JSGPB DAKCP MQRGM MBXDT NAULS MYJRI USVAY WQGUK KEWRJ BAPPW YDWQU KFDHC OOOWF QVANE XLEEK MVFBX HYQOR SFKGU AKWEB LEPXV LHRCG MKMSO DVOZS JFESS LTUEY QUGAA IODSI IZEQJ ROTBS TKSEH JBORC ZZNVH EOOAA"}

{"flag": "GGMCT NJOAA QAEYB FJZLP VKZTA DHIIG RVYGC RPQQN LHWRR YSDXM YDSJL ZUROG KHXNX DGPSM PPEBK INKSS WEVSH ZNEKW OTZNR NFLYQ KLIRC JVWLI PSNBF OEFHC NDUVO CABZC LCTEN NMDSI XVDEL DRADR YIPBQ IKOLM DJAQA GGMCT NJOAA"}

{"flag": "IISNJ IFFAA TYPMO WDJHA ZMNBD LKUAY TYPVD UGAYU OQMOO YRVUS SLFZI IXKVW LYUGT JWTYV XNEYU HLQVV IXUMJ BKNUQ WMLQT QKIWV UXOCA CVSPG UKJQG XCSFI RJEKU BWLBM AVRFW DMOPT VFXTD VROND XSEHF ZLWEJ VOVSX IISNJ IFFAA"}

{"flag": "BBHAC QDFAA KGBMH RVZSK RNVZH NGRAM WYHHE HKHJU UCQBL HPVAP TXDCZ ZMKWX ETCKC CMBSC VKUUF BMAIV RTAJE EWOUS SMOTQ KNQBF IRDVZ YJWQK WEAIA TONBI MMBUI RCULP BKEIO LNOAM XLUDR XJYAM DMWJN DUXXV FDVOC BBHAC QDFAA"}

Thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import requests
from string import ascii_uppercase

ct = 'QAEYBFJZLPVKZTADHIIGRVYGCRPQQNLHWRRYSDXMYDSJLZUROGKHXNXDGPSMPPEBKINKSSWEVSHZNEKWOTZNRNFLYQKLIRCJVWLIPSNBFOEFHCNDUVOCABZCLCTENNMDSIXVDELDRADRYIPBQIKOLMDJAQA'
print(ct)


def rua(c, i):
    pre = "A" * i

    for ch in ascii_uppercase:
        cipher = requests.post("http://03.cr.yp.toc.tf:11117/m209/encipher",
                               data={
                                   "plain": pre + ch
                               }).json()["cipher"]

        cipher = cipher.replace(" ", "")[10:-10]        # remove head and tail
        print(cipher)
        if cipher[i] == c:
            print('flag[i] is', ch)
            return ch


flag = ""

for i, c in enumerate(ct):
    flag += rua(c, i)
    print(flag)

result

medium

Aniely

分值：66

考点：爆破

challenge

There is stream cipher, try to keep it smooth!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#!/usr/bin/env python3

from struct import *
from os import *
from secret import passphrase, flag

def aniely_stream(passphrase):
	def mixer(u, v):
		return ((u << v) & 0xffffffff) | u >> (32 - v)

	def forge(w, a, b, c, d):
		for i in range(2):
			w[a] = (w[a] + w[b]) & 0xffffffff
			w[d] = mixer(w[a] ^ w[d], 16 // (i + 1))
			w[c] = (w[c] + w[d]) & 0xffffffff
			w[b] = mixer(w[b] ^ w[c], (12 + 2*i) // (i + 1))

	bring = [0] * 16
	bring[:4] = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]
	bring[4:12] = unpack('<8L', passphrase)
	bring[12] = bring[13] = 0x0
	bring[14:] = [0] * 2

	while True:
		w = list(bring)
		for _ in range(10):
			forge(w, 0x0, 0x4, 0x8, 0xc)
			forge(w, 0x1, 0x5, 0x9, 0xd)
			forge(w, 0x2, 0x6, 0xa, 0xe)
			forge(w, 0x3, 0x7, 0xb, 0xf)
			forge(w, 0x0, 0x5, 0xa, 0xf)
			forge(w, 0x1, 0x6, 0xb, 0xc)
			forge(w, 0x2, 0x7, 0x8, 0xd)
			forge(w, 0x3, 0x4, 0x9, 0xe)
		for c in pack('<16L', *((w[_] + bring[_]) & 0xffffffff for _ in range(16))):
			yield c
		bring[12] = (bring[12] + 1) & 0xffffffff
		if bring[12] == 0:
			bring[13] = (bring[13] + 1) & 0xffffffff

def aniely_encrypt(msg, passphrase):
	if len(passphrase) < 32:
		passphrase = (passphrase * (32 // len(passphrase) + 1))[:32]
	rand = urandom(2) * 16
	return bytes(a ^ b ^ c for a, b, c in zip(msg, aniely_stream(passphrase), rand))

key = bytes(a ^ b for a, b in zip(passphrase, flag))
enc = aniely_encrypt(passphrase, key)
print(f'key = {key.hex()}')
print(f'enc = {enc.hex()}')

Thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#!/usr/bin/env python3

from struct import *

key = 0x4dcceb8802ae3c45fe80ccb364c8de19f2d39aa8ebbfb0621623e67aba8ed5bc
enc = 0xe67a67efee3a80b66af0c33260f96b38e4142cd5d9426f6f156839f2e2a8efe8
from os import urandom
from Crypto.Util.number import *

def aniely_stream(passphrase):
	def mixer(u, v):
		return ((u << v) & 0xffffffff) | u >> (32 - v)

	def forge(w, a, b, c, d):
		for i in range(2):
			w[a] = (w[a] + w[b]) & 0xffffffff
			w[d] = mixer(w[a] ^ w[d], 16 // (i + 1))
			w[c] = (w[c] + w[d]) & 0xffffffff
			w[b] = mixer(w[b] ^ w[c], (12 + 2*i) // (i + 1))

	bring = [0] * 16
	bring[:4] = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]
	bring[4:12] = unpack('<8L', passphrase)
	bring[12] = bring[13] = 0x0
	bring[14:] = [0] * 2

	while True:
		w = list(bring)
		for _ in range(10):
			forge(w, 0x0, 0x4, 0x8, 0xc)
			forge(w, 0x1, 0x5, 0x9, 0xd)
			forge(w, 0x2, 0x6, 0xa, 0xe)
			forge(w, 0x3, 0x7, 0xb, 0xf)
			forge(w, 0x0, 0x5, 0xa, 0xf)
			forge(w, 0x1, 0x6, 0xb, 0xc)
			forge(w, 0x2, 0x7, 0x8, 0xd)
			forge(w, 0x3, 0x4, 0x9, 0xe)
		for c in pack('<16L', *((w[_] + bring[_]) & 0xffffffff for _ in range(16))):
			yield c
		bring[12] = (bring[12] + 1) & 0xffffffff
		if bring[12] == 0:
			bring[13] = (bring[13] + 1) & 0xffffffff

passphrase = long_to_bytes(key)
msg = long_to_bytes(enc)
for i in range(256**2):
	rand = long_to_bytes(i,2)*16
	s = bytes(a ^ b ^ c for a, b, c in zip(msg, aniely_stream(passphrase), rand))
	flag = bytes(a ^ b for a, b in zip(passphrase, s))
	if b"CCTF" in flag:
		print(flag)

result

1
b'CCTF{7rY_t0_D3cRyPT_z3_ChaCha20}'

Diploma

分值：71

考点：

challenge

We are trying to solve matrix problem with only diploma! Here we go around the matrix!

1
nc 08.cr.yp.toc.tf 37313
1
2
3
4
5
6
7
8
9
10
11
12
13
[root@VM-0-7-centos ~]# nc 08.cr.yp.toc.tf 37313
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  Hi all, cryptographers know that the calculation of the order of a  |
|  given element in a group is not easy at all. We are working in the  |
|  group GL(d, p), the group of invertible matrices of order `d' on a  |
|  finite field of order `p'. In each stage send the order matrix M.   |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Generating the parameters for p = 127, please wait...
| M = 
[ 14  34  93]
[104 124 111]
[ 35  34  37] 
| Send the order of matrix M:

Thought

1
sage: M.multiplicative_order()

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import re
from gmpy2 import iroot
from pwn import *
context.log_level = 'debug'
sh = remote("08.cr.yp.toc.tf",37313)

def format(s):
	value = re.findall(".*?(\\d+).*?",s)
	print(len(value))
	length = iroot(len(value),int(2))[0]
	m=[]
	for i in range(length):
		mm=[]
		for j in range(length):
			mm.append(int(value[i*length+j]))
		m.append(mm)
	return m

for i in range(20):
	sh.recvuntil("M = ")
	s = sh.recvuntil("Send the order")
	m = format(s.decode())
	M = Matrix(GF(127),m)
	sh.sendline(str(M.multiplicative_order()))

result

1
b'| Congrats, you got the flag: CCTF{ma7RicES_4R3_u5EfuL_1n_PUbl!c-k3y_CrYpt0gr4Phy!}\n'

Oak land

分值：122

考点：离散对数

challenge

Where to publish the great work!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

p = 7389313481223384214994762619823300589978423075857540712007981373887018860174846208000957230283669342186460652521580595183523706412588695116906905718440770776239313669678685198683933547601793742596023475603667
e = 31337
f = 7236042467316654159796543399639966340258093274047941788600980451877044636122969830708918356119442228154447395855689559447196348683125675305629837437591088260218138895919514078948650757100432223219969122629790
g = 1878626136321051642174045874618248475160620873585704351202865003185878331837410979441756843820270907300810543618813757245154196050399357659526631164136221434463496532263979506870318259276669412698827040743576

x = bytes_to_long(flag.encode('utf-8'))
assert x < p
c = (110 * pow(e, x, p) + 313 * pow(f, x, p) + 114 * pow(g, x, p)) % p
print(f'c = {c}')

Thought

$c \equiv 110 \cdot e^x + 313 \cdot f^x+114\cdot g^x \pmod p$

$\to f \equiv e^y ,g \equiv e^z $

$\to c \equiv 110 \cdot e^{x} + 313 \cdot e^{xy} + 114 \cdot e^{xz} \pmod p$

$\to c \equiv 110 \cdot e^x + 313 \cdot e^{-x} + 114 \cdot e^{-2x} \pmod p$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
c = 871346503375040565701864845493751233877009611275883500035764036792906970084258238763963152627486758242101207127598485219754255161617890137664012548226251138485059295263306930653899766537171223837761341914356
p = 7389313481223384214994762619823300589978423075857540712007981373887018860174846208000957230283669342186460652521580595183523706412588695116906905718440770776239313669678685198683933547601793742596023475603667
e = 31337
f = 7236042467316654159796543399639966340258093274047941788600980451877044636122969830708918356119442228154447395855689559447196348683125675305629837437591088260218138895919514078948650757100432223219969122629790
g = 1878626136321051642174045874618248475160620873585704351202865003185878331837410979441756843820270907300810543618813757245154196050399357659526631164136221434463496532263979506870318259276669412698827040743576

R.<x> = Zmod(p)[]

f = 110 * x^3 + 313 * x +114 - c*x^2

x0 = f.roots()[0][0]

flag = discrete_log(Mod(x0,p),Mod(e,p))
from Crypto.Util.number import *
print(long_to_bytes(flag))

result

1
b'CCTF{V33333rY_eeeeZy_DLP_cH41L3n9E!}'

Cantilever

分值：79

考点：$p-1 \ is \ smooth$

challenge

What if you can find the message? If you can, that means you are genius, because we harden our crypto system with a very modern tool!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

def gen_primes(nbit, imbalance):
	p = 2
	FACTORS = [p]
	while p.bit_length() < nbit - 2 * imbalance:
		factor = getPrime(imbalance)
		FACTORS.append(factor)
		p *= factor
	rbit = (nbit - p.bit_length()) // 2

	while True:
		r, s = [getPrime(rbit) for _ in '01']
		_p = p * r * s
		if _p.bit_length() < nbit: rbit += 1
		if _p.bit_length() > nbit: rbit -= 1
		if isPrime(_p + 1):
			FACTORS.extend((r, s))
			p = _p + 1
			break

	FACTORS.sort()
	return (p, FACTORS)

def genkey(nbit, imbalance, e):
	while True:
		p, FACTORS = gen_primes(nbit // 2, imbalance)
		if len(FACTORS) != len(set(FACTORS)):
			continue
		q, q_factors = gen_primes(nbit // 2, imbalance + 1)
		if len(q_factors) != len(set(q_factors)):
			continue
		factors = FACTORS + q_factors
		if e not in factors:
			break
	n = p * q
	return n, (p, q)

nbit = 2048
imbalance = 19
e = 0x10001

m_1 = bytes_to_long(flag[:len(flag) // 2])
m_2 = bytes_to_long(flag[len(flag) // 2:])

n, PRIMES = genkey(nbit, imbalance, e)

c_1 = pow(m_1, e, n)
c_2 = pow(e, m_2, n)

print(f'n = {n}')
print(f'c_1 = {c_1}')
print(f'c_2 = {c_2}')

Thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#!/usr/bin/env python3

from Crypto.Util.number import *

def gen_primes(nbit, imbalance):
	p = 2
	FACTORS = [p]
	while p.bit_length() < nbit - 2 * imbalance:
		factor = getPrime(imbalance)
		FACTORS.append(factor)
		p *= factor
	rbit = (nbit - p.bit_length()) // 2
	print(rbit)
	while True:
		r, s = [getPrime(rbit) for _ in '01']
		_p = p * r * s
		if _p.bit_length() < nbit: rbit += 1
		if _p.bit_length() > nbit: rbit -= 1
		if isPrime(_p + 1):
			FACTORS.extend((r, s))
			p = _p + 1
			break

	FACTORS.sort()
	print(FACTORS)
	return (p, FACTORS)

def genkey(nbit, imbalance, e):
	while True:
		p, FACTORS = gen_primes(nbit // 2, imbalance)
		if len(FACTORS) != len(set(FACTORS)):
			continue
		q, q_factors = gen_primes(nbit // 2, imbalance + 1)
		if len(q_factors) != len(set(q_factors)):
			continue
		factors = FACTORS + q_factors
		if e not in factors:
			break
	n = p * q
	return n, (p, q)

nbit = 2048
imbalance = 19
e = 0x10001	
#n, PRIMES = genkey(nbit, imbalance, e)

from gmpy2 import *
from tqdm import tqdm
def Pollard_p_1(N):
	print("[+]Trying Pollard's p-1...\n")
	a = 2
	while True:
		f = a
		# precompute
		for n in tqdm(range(1, 887651)):
			f = powmod(f, n, N)
		for n in tqdm(range(887651, 10466421)):
			f = powmod(f, n, N)
			if n % 15 == 0:
				p = gcd(f-1, N)
				if 1 < p < N:
					q = N // p
					print("p: ", p)
					print("q: ", q)
					return p,q
N=7069789930583271525053215046247773438899869283661158227309691853515987055334306019600324056376312479212090202373516405860759222837585952590589336295698718699890424169542280710721069784487366121478569760563045886361884895363592898476736269784284754788133722060718026577238640218755539268465317292713320841554802703379684173485217045274942603346947299152498798736808975912326592689302969859834957202716983626393365387411319175917999258829839695189774082810459527737342402920881184864625678296442001837072332161966439361793009893108796934406114288057583563496587655548536011677451960307597573257032154009427010069578913
#Pollard_p_1(N)
from Crypto.Util.number import *

p=83408372012221120677052349409462320990177094246143674474872152829440524098582262384066400107950985845255268335597502228206679771838750219696329523257176739436871327238322817403970284015587320158034304282786944710043150568360761457471641695390427267786485448748458445872307883254297662715749746270343116946519
q=84761154786085445040051273337185621770653977624442810400422736258693219544281946893222923335092616440575888204882883202879374137962201839964482318483860286412488851522612902055732831909496637360268825720155284438779235801463340052531340653630637729255285872455686692027630814695155220888112228977346697309127
c_1 = 488692928085934899944055554857568564903346089951134051486941368561567330884363274156339625953702601270565654444836193796061118053575538224794730472032345171432952984560662218697488844007827176184413713651118743456250147472678673801728916283759932987216388378211555067885210167894310696549664382751443669387953644382833924884208966436685137553434532738845959014828804809425096115758364136546390809453200055265653531950423111482644330073443545410319576097902472017235065047191133112557289289189187696092145850680765843608118584107829268136014912479701945735063525799796920293418182776436767911172221104640501952880057
c_2 = 109770827223661560471527567179288748906402603483328748683689436879660543465776899146036833470531024202351087008847594392666852763100570391337823820240726499421306887565697452868723849092658743267256316770223643723095601213088336064635680075206929620159782416078143076506249031972043819429093074684182845530529249907297736582589125917235222921623698038868900282049587768700860009877737045693722732170123306528145661683416808514556360429554775212088169626620488741903267154641722293484797745665402402381445609873333905772582972140944493849645600529147490903067975300304532955461710562911203871840101407995813072692212
e = 0x10001
d = inverse(e,(p-1)*(q-1))
m1 = long_to_bytes(pow(c_1,d,p*q))

m2p = discrete_log(Mod(c_2,p),Mod(e,p))
m2q = discrete_log(Mod(c_2,q),Mod(e,q))
print(m1+long_to_bytes(crt([m2p,m2q],[p,q])))

result

1
b'CCTF{5L3Ek_4s__s1lK__Ri9H7?!}'

Side step

分值：146

考点：“侧信道”

challenge

I like to have my own pow!

1
2
3
nc 01.cr.yp.toc.tf 17331
nc 02.cr.yp.toc.tf 17331
nc 03.cr.yp.toc.tf 17331
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#!/usr/bin/env python3

from Crypto.Util.number import *
import random, sys
from flag import flag

def pow_d(g, e, n):
	t, r = 0, 1
	for _ in bin(e)[2:]:
		if r == 4: t += 1
		r = pow(r, 2, n)
		if _ == '1': r = r * g % n
	return t, r

def ts(m, p):
	m = m % p
	return pow(m, (p - 1) // 2, p) == 1

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Hi all cryptographers! Welcome to the Sidestep task, we do powing!!!", border)
	pr(border, "You should solve a DLP challenge in some special way to get the flag", border)

	p = 2 ** 1024 - 2 ** 234 - 2 ** 267 - 2 ** 291 - 2 ** 403 - 1
	s = random.randint(2, (p - 1) // 2)

	while True:
		pr("| Options: \n|\t[T]ry the magic machine \n|\t[Q]uit")
		ans = sc().lower()

		if ans == 't':
			pr(border, "please send your desired integer: ")
			g = sc()
			try:
				g = int(g)
			except:
				die(border, "The given input is not integer!")
			if ts(g, p):
				t, r = pow_d(g, s, p)
				if r == 4:
					die(border, f'Great! you got the flag: {flag}')
				else:
					pr(border, f"t, r = {t, r}")
			else:
				pr(border, "The given base is NOT valid!!!")
		elif ans == 'q':
			die(border, "Quitting ...")
		else:
			die(border, "Bye bye ...")

if __name__ == "__main__":
	main()

Thought

1
if r == 4: t += 1

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import re
from gmpy2 import iroot
from tqdm import *
from pwn import *

sh = remote("01.cr.yp.toc.tf",17331)

p = 2 ** 1024 - 2 ** 234 - 2 ** 267 - 2 ** 291 - 2 ** 403 - 1
x = Mod(2,p)
s="1"

for i in tqdm(range(0,1024)):
	if int(s,2) >= (p-1)//2:
		break
	sh.recvuntil("[Q]uit\n")
	sh.sendline("T")
	sh.recvuntil("integer: \n")
	sh.sendline(str(x.nth_root(int(s,2))))
	FLAG = sh.recvuntil("\n")[:-1]
	if b"Great!" in FLAG:
		print(FLAG)
		exit()
	else:
		t,r = eval(FLAG[9:])
		#print(t,r)
	if r==2:
		break
	if t == 1:
		s+="0"
	elif t == 0:
		s+="1"
	else:
		print(FLAG)

sh.recvuntil("[Q]uit\n")
sh.sendline("T")
sh.recvuntil("integer: \n")
sh.sendline(str((2*x).nth_root(int(s,2))))
FLAG = sh.recvuntil("\n")[:-1]
print(FLAG)

result

1
b'| Great! you got the flag: CCTF{h0W_iZ_h4rD_D15crEt3_lO9ar!Thm_c0nJec7ur3?!}'

Faonsa *

分值：180

考点：

challenge

Deploying the fault attack in real life is hard, we deployed it artificially!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#!/usr/bin/env python3

from Crypto.Util.number import *
from math import gcd
import sys
from flag import flag

def diff(a, b):
	assert a.bit_length() == b.bit_length()
	w, l = 0, a.bit_length()
	for _ in range(l):
		if bin(a)[2:][_] != bin(b)[2:][_]: w += 1
	return w

def sign_esa(pubkey, x, m):
	g, p, y = pubkey
	while True:
		k = getRandomRange(2, p-1)
		if gcd(k, p-1) == 1:
			break
	u = pow(g, k, p)
	v = (m - x * u) * inverse(k, p - 1) % (p - 1)
	return (u, v)

def verify_esa(pubkey, sgn, m):
	g, p, y = pubkey
	u, v = sgn
	return pow(y, u, p) * pow(u, v, p) % p == pow(g, m, p)

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Hello guys! This is a another challenge on fault attack too, again  ", border)
	pr(border, "our storage could apply at most `l' bit fault on ElGamal modulus, p,", border)
	pr(border, "try to sign the given message and get the flag! Have fun and enjoy!!", border)
	pr(border*72)
	pr(border, "Generating the parameters, it's time consuming ...")
	nbit = 256
	while True:
		_p = getPrime(255)
		p = 2 * _p + 1
		if isPrime(p):
			g = 2
			if pow(g, _p, p) != 1: break
			else: g += 1
	x = getRandomRange(2, p // 2)
	y = pow(g, x, p)

	B, l = [int(b) for b in bin(p)[2:]], 30
	
	MSG = "4lL crypt0sy5t3ms suck5 fr0m faul7 atTaCk5 :P"
	m = bytes_to_long(MSG.encode('utf-8'))

	while True:
		pr("| Options: \n|\t[A]pply fault \n|\t[G]et the parameters \n|\t[S]ign the message \n|\t[V]erify the signature \n|\t[Q]uit")
		ans = sc().lower()
		if ans == 'a':
			_B = B
			pr(border, f"please send at most {l}-tuple array from indices of bits of ElGamal modulus, like: 5, 12, ...")
			ar = sc()
			try:
				ar = [int(_) for _ in ar.split(',')]
				if len(ar) <= l:
					for i in range(len(ar)): 
						_B[ar[i]] = (_B[ar[i]] + 1) % 2
					P = int(''.join([str(b) for b in _B]), 2)
					Y = pow(g, x, P)
				else: raise Exception('Invalid length!')
			except: pr(border, "Something went wrong!!")
		elif ans == 'g':
			pr(border, f'p = {p}')
			pr(border, f'g = {g}')
			pr(border, f'y = {y}')
		elif ans == "v":
			pr(border, "please send signature to verify: ")
			_flag, signature = False, sc()
			try:
				signature = [int(_) for _ in signature.split(',')]
				if verify_esa((g, P, Y), signature, m): _flag = True
				else: pr(border, "Your signature is not valid!!")
			except:
				pr(border, "Something went wrong!!")
			if _flag: die(border, "Congrats! your got the flag: " + flag)
		elif ans == 's':
			pr(border, "Please send your message to sign: ")
			msg = sc().encode('utf-8')
			if msg != MSG.encode('utf-8'):
				_m = bytes_to_long(msg)
				try:
					sgn = sign_esa((g, P, Y), x, _m)
					pr(border, f'sign = {sgn}')
				except:
					pr(border, "Something went wrong!!")
			else:
				pr(border, "Kidding me!? Really?")
		elif ans == 'q': die("Quitting ...")
		else: die("Bye bye ...")

if __name__ == "__main__": main()

Thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from sympy import isprime
from Crypto.Util.number import *
import re
from tqdm import *
from pwn import *

sh = remote("06.cr.yp.toc.tf",31117)
sh.recvuntil("[Q]uit")
sh.sendline("G")
sh.recvuntil("| p = ")
p = int(sh.recvuntil("\n")[:-1])
print("[+] p = ",p)
s = bin(p)[2:].rjust(256,'0')
sl = list(s)
for i in range(256):
	sll = sl.copy()
	sll[i] = str((int(sll[i]) + 1) % 2)
	ss = ''.join(i for i in sll)
	ss = int(ss,2)
	if isprime(ss):
		print("[+] i = ",i)
		MSG = "4lL crypt0sy5t3ms suck5 fr0m faul7 atTaCk5 :P"
		m = bytes_to_long(MSG.encode('utf-8'))
		sh.recvuntil("[Q]uit")
		sh.sendline("A")
		sh.recvuntil("...\n")
		sh.sendline(str(i))
		sh.recvuntil("[Q]uit")
		sh.sendline("S")
		sh.recvuntil("sign: \n")
		sh.sendline("\x004lL crypt0sy5t3ms suck5 fr0m faul7 atTaCk5 :P")
		sh.recvuntil("sign = (")
		data = sh.recvuntil(")")[:-1]
		sh.recvuntil("[Q]uit")
		sh.sendline("V")
		sh.recvuntil("verify: ")
		sh.sendline(data)
		sh.interactive()

result

1
Congrats! your got the flag: CCTF{n3W_4t7aCk_8y_fAuL7_!nJ3cT10N_oN_p!!!}

Resign

分值：122

考点：RSA，离散对数

challenge

Everything is up to you, I just want it to be verified!

1
nc 03.cr.yp.toc.tf 11137

Thought

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#!/usr/bin/env python3

from Crypto.Util.number import *


def gen_primes(nbit, imbalance):
	p = 2
	FACTORS = [p]
	while p.bit_length() < nbit - 2 * imbalance:
		factor = getPrime(imbalance)
		FACTORS.append(factor)
		p *= factor
	rbit = (nbit - p.bit_length()) // 2

	while True:
		r, s = [getPrime(rbit) for _ in '01']
		_p = p * r * s
		if _p.bit_length() < nbit: rbit += 1
		if _p.bit_length() > nbit: rbit -= 1
		if isPrime(_p + 1):
			FACTORS.extend((r, s))
			p = _p + 1
			break

	FACTORS.sort()
	return (p, FACTORS)

def genkey(nbit, imbalance, e):
	while True:
		p, FACTORS = gen_primes(nbit // 2, imbalance)
		if len(FACTORS) != len(set(FACTORS)):
			continue
		q, q_factors = gen_primes(nbit // 2, imbalance + 1)
		if len(q_factors) != len(set(q_factors)):
			continue
		factors = FACTORS + q_factors
		if e not in factors:
			break
	print(p.bit_length(),q.bit_length())
	n = p * q
	return n, (p, q)

nbit = 2048
imbalance = 16
e = 0x10001


n, PRIMES = genkey(nbit, imbalance, e)
print(PRIMES)

#!/usr/bin/env sage
from pwn import *
from Crypto.Util.number import *
from hashlib import sha1
context.log_level = 'debug'

sh = remote("03.cr.yp.toc.tf",11137)
sh.recvuntil("[Q]uit\n")
sh.sendline("P")
sh.recvuntil("SIGN = ")
MSG = b'::. Can you forge any signature? .::'
h = bytes_to_long(sha1(MSG).digest())


SIGN = int(sh.recvuntil("\n")[:-1])
print('[+] SIGN',SIGN)

p = 111657144993852623256233363989000281515390441372107528881614340689818824455290685121511873461605564810943387707541782379213899558901650423480949095316252223627543325756537840564774645148163170125669641536489937366637706602313785316184656176701603589042384374855568020323292801352393162697967354397541828173999
q = 137452291102384188629897087949133529139596156344413834145488477828519011767513127595258850210995836074279851378837357321395849566085251970484428954340841155028617799079020425268855055662977244431658824300349726299807123259984818563478362175002364805620517750136398917859466563648383901744997103947168570641187

hp = Mod(h,p)
hq = Mod(h,q)
SIGNp = Mod(SIGN,p)
SIGNq = Mod(SIGN,q)
dp = discrete_log(SIGNp,hp)
dq = discrete_log(SIGNq,hq)

d = crt([dp,dq],[p-1,q-1])

if int(pow(h,d,p*q)) == SIGN:
	if GCD(d,(p-1)*(q-1)) == 1:
		print("fxxk")
		e = inverse(d,(p-1)*(q-1))
		sh.recvuntil("[Q]uit")
		sh.sendline("G")
		sh.recvuntil("e, p, q: \n")
		sh.sendline(str(e)+','+str(p)+','+str(q))
		sh.recvuntil("[Q]uit")
		sh.sendline("S")
		sh.recvuntil("signature?'\n")
		MSG = b'Can you forge any signature?'
		h = bytes_to_long(sha1(MSG).digest())
		SIGN = pow(h,d,p*q)
		sh.sendline(str(SIGN))
		sh.interactive()

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
DEBUG] Received 0x124 bytes:
    b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n'
    b'|  Hi, Try to guess our RSA private key to sign my message, talented   |\n'
    b'|  hackers like you ;) are able to do it, they are *Super Guesser* :)  |\n'
    b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n'
[DEBUG] Received 0x79 bytes:
    b'| Options: \n'
    b'|\t[G]uess the secret key \n'
    b'|\t[R]eveal the parameters \n'
    b'|\t[S]ign the message \n'
    b'|\t[P]rint the signature \n'
    b'|\t[Q]uit\n'
b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n|  Hi, Try to guess our RSA private key to sign my message, talented   |\n|  hackers like you ;) are able to do it, they are *Super Guesser* :)  |\n||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n| Options: \n|\t[G]uess the secret key \n|\t[R]eveal the parameters \n|\t[S]ign the message \n|\t[P]rint the signature \n|\t[Q]uit\n'
[DEBUG] Sent 0x2 bytes:
    b'P\n'
[DEBUG] Received 0x2eb bytes:
    b'| SIGN = 1884979486179267172629071748772960684525918761368459562494944521319157361276555864681125909692176171908421490752034980705358031300244785204930649379956166150325630173523685712244072241350875975367044434668751487177083506342445469016490120622963393427220812176101874623720018150321035528311870301905555456217022341243237754724758138283713012282683466454035765617272995819418670105072095751108482305696064164203703964113835533643311960967384709366019160090937911359945847278007091075054690456979913301969543047273265630157888695674988233511928839475589794274485590101615174673363075114406219602464625105663962079644520\n'
    b'| Options: \n'
    b'|\t[G]uess the secret key \n'
    b'|\t[R]eveal the parameters \n'
    b'|\t[S]ign the message \n'
    b'|\t[P]rint the signature \n'
    b'|\t[Q]uit\n'
b'| SIGN = '
[+] SIGN 1884979486179267172629071748772960684525918761368459562494944521319157361276555864681125909692176171908421490752034980705358031300244785204930649379956166150325630173523685712244072241350875975367044434668751487177083506342445469016490120622963393427220812176101874623720018150321035528311870301905555456217022341243237754724758138283713012282683466454035765617272995819418670105072095751108482305696064164203703964113835533643311960967384709366019160090937911359945847278007091075054690456979913301969543047273265630157888695674988233511928839475589794274485590101615174673363075114406219602464625105663962079644520
fxxk
b'| Options: \n|\t[G]uess the secret key \n|\t[R]eveal the parameters \n|\t[S]ign the message \n|\t[P]rint the signature \n|\t[Q]uit'
[DEBUG] Sent 0x2 bytes:
    b'G\n'
[DEBUG] Received 0x58 bytes:
    b'| please send the RSA public exponent and PARAMS p, q separated by comma like e, p, q: \n'
b'\n| please send the RSA public exponent and PARAMS p, q separated by comma like e, p, q: \n'
[DEBUG] Sent 0x4d5 bytes:
    b'1082509150456156106884081968159156913760335792759806098810796864909671429408421841803533150740116700026128780447868696484459882205449338489621368675729546554138586645439999758864564356677551698788758655342144120696616357464766656368816629053686382888005864636070497927528775619554284621090631929298361123902250120620368264008458905321583778273487521490405775436737576378858039231200324269802397928442682665991885792951426166328402109317610419406523068126450035524015631711806220255873191159798260905167582006341922779876987929771318339923632673933137592828056519016523309961026716569844436949376058435508905723342417,111657144993852623256233363989000281515390441372107528881614340689818824455290685121511873461605564810943387707541782379213899558901650423480949095316252223627543325756537840564774645148163170125669641536489937366637706602313785316184656176701603589042384374855568020323292801352393162697967354397541828173999,137452291102384188629897087949133529139596156344413834145488477828519011767513127595258850210995836074279851378837357321395849566085251970484428954340841155028617799079020425268855055662977244431658824300349726299807123259984818563478362175002364805620517750136398917859466563648383901744997103947168570641187\n'
[DEBUG] Received 0xb0 bytes:
    b'| Great guess, now you are able to sign any message!!!\n'
    b'| Options: \n'
    b'|\t[G]uess the secret key \n'
    b'|\t[R]eveal the parameters \n'
    b'|\t[S]ign the message \n'
    b'|\t[P]rint the signature \n'
    b'|\t[Q]uit\n'
b'| Great guess, now you are able to sign any message!!!\n| Options: \n|\t[G]uess the secret key \n|\t[R]eveal the parameters \n|\t[S]ign the message \n|\t[P]rint the signature \n|\t[Q]uit'
[DEBUG] Sent 0x2 bytes:
    b'S\n'
[DEBUG] Received 0x56 bytes:
    b'| Please send the signature of this message: \n'
    b"| MSG = b'Can you forge any signature?'\n"
b"\n| Please send the signature of this message: \n| MSG = b'Can you forge any signature?'\n"
[DEBUG] Sent 0x269 bytes:
    b'6405963942855203301347394631014609423992976281972065881342338496966442578053021980219447404666870923023663382787130224892392393868461338946121986093285771246460632133140203751153251832618215496457946029937232569540657082525075384223510445529041161208578664500813584918972603341691293142627717376172706084401258955031379528849034321969314268480220168916307424094843069609226093174228181505421177268243717352042515478881472086430474238444194579059472586968454225397094847478032233134598568589612408572830610570087471515907683694823038385520728023957596495473215173554090359646138552942072568176241390134476189114424111\n'
[*] Switching to interactive mode
[DEBUG] Received 0x4a bytes:
    b'| Congrats! your got the flag: CCTF{Unkn0wN_K3y_5h4rE_4t7aCk_0n_Th3_RSA!}\n'
| Congrats! your got the flag: CCTF{Unkn0wN_K3y_5h4rE_4t7aCk_0n_Th3_RSA!}

DBB

分值：103

考点：椭圆曲线poh-hellman

challenge

Old school but fun hopscotch!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#!/usr/bin/env sage

from Crypto.Util.number import *
from secret import n, B, BASE_POINT, FLAG

m = bytes_to_long(FLAG)
assert m < n

F = IntegerModRing(n)
E = EllipticCurve(F, [31337, B])

BASE_POINT = E(BASE_POINT)

P = m * BASE_POINT
print(f'n = {n}')
print(f'BASE_POINT.x = {BASE_POINT.xy()[0]}')
print(f'P = {P.xy()[0], P.xy()[1]}')


# n = 34251514713797768233812437040287772542697202020425182292607025836827373815449
# BASE_POINT.x = 7331
# P = (10680461779722115247262931380341483368049926186118123639977587326958923276962, 4003189979292111789806553325182843073711756529590890801151565205419771496727)

Thought

$n= 11522256336953175349 \cdot 14624100800238964261 \cdot 203269901862625480538481088870282608241$

“子曲线：”

$m \cdot G \equiv Y \pmod n \to m \cdot G \equiv Y \pmod p \ if \ (p \mid n)$

PS：CRT的时候有坑

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
n = 34251514713797768233812437040287772542697202020425182292607025836827373815449
xx= 10680461779722115247262931380341483368049926186118123639977587326958923276962
yy= 4003189979292111789806553325182843073711756529590890801151565205419771496727
n = 34251514713797768233812437040287772542697202020425182292607025836827373815449
A = 31337
B = (yy^2 - xx^3 - A*xx) % n


p = 11522256336953175349
q = 14624100800238964261
r = 203269901862625480538481088870282608241
p1=p
p2=q
p3=r
F = IntegerModRing(n)
E = EllipticCurve(F, [A, B])
T = E(xx,yy)
assert p*q*r == n

Fp = IntegerModRing(p)
Ep = EllipticCurve(Fp, [A, B])
Tp = Ep(xx,yy)
R.<y> = Zmod(p)[]
x = 7331
f = y^2 -  x^3 - A*x - B
yp0 = f.roots()[0][0]
yp1 = f.roots()[1][0]
Gp0 = Ep(x,yp0)
Gp1 = Ep(x,yp1)
mp1 = discrete_log(Tp,Gp0,operation='+')
mp2 = discrete_log(Tp,Gp1,operation='+')

Fq = IntegerModRing(q)
Eq = EllipticCurve(Fq, [A, B])
Tq = Eq(xx,yy)
R.<y> = Zmod(q)[]
x = 7331
f = y^2 -  x^3 - A*x - B
yq0 = f.roots()[0][0]
yq1 = f.roots()[1][0]
Gq0 = Eq(x,yq0)
Gq1 = Eq(x,yq1)
mq1 = discrete_log(Tq,Gq0,operation='+')
mq2 = discrete_log(Tq,Gq1,operation='+')


Fr = IntegerModRing(r)
Er = EllipticCurve(Fr, [A, B])
Tr = Er(xx,yy)
R.<y> = Zmod(r)[]
x = 7331
f = y^2 -  x^3 - A*x - B
yr0 = f.roots()[0][0]
yr1 = f.roots()[1][0]
Gr0 = Er(x,yr0)
Gr1 = Er(x,yr1)
mr1 = discrete_log(Tr,Gr0,operation='+')
mr2 = discrete_log(Tr,Gr1,operation='+')

from Crypto.Util.number import *


EP = Ep.order()
EQ = Eq.order()
ER = Er.order()
for mp in [mp1,mp2]:
    for mq in [mq1,mq2]:
        for mr in [mr1,mr2]:
            m = crt([mp,mq,mr],[EP//GCD(mp,EP),EQ//GCD(mq,EQ),ER//GCD(mr,ER)])
            if b"CCTF" in long_to_bytes(m):
                print(long_to_bytes(m))

result

Fiercest

分值：142

考点：

challenge

Once again, we decided to deploy an artificial fault attack!

1
nc 04.cr.yp.toc.tf 37713

Thought

diff(n,nextprime(n)) <= 2

$d \equiv e^{-1} \pmod {nextprime(n)-1}$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from sympy import *
from Crypto.Util.number import *
from pwn import *

context.log_level = 'debug'
def diff(a, b):
	assert a.bit_length() == b.bit_length()
	w, l = 0, a.bit_length()
	L = []
	for _ in range(l):
		if bin(a)[2:][_] != bin(b)[2:][_]: 
			w += 1
			L.append(_)
	if w<=2:
		print(L)
	return w,L


for index in range(100):
	print(index)
	sh = remote("04.cr.yp.toc.tf","37713")

	sh.recvuntil("[Q]uit\n")
	sh.sendline("G")
	sh.recvuntil("n = ")
	n = int(sh.recvuntil("\n")[:-1])
	w,L = diff(n,nextprime(n))
	if(w)<=2:
		sh.recvuntil("[Q]uit\n")
		sh.sendline("A")
		sh.recvuntil("\n")
		sh.sendline(str(L)[1:-1])
		sh.recvuntil("[Q]uit\n")
		sh.sendline("V")
		sh.recvuntil("\n")
		MSG = "4lL crypt0sy5t3ms suck5 fr0m faul7 atTaCk5 :P"
		m = bytes_to_long(MSG.encode('utf-8'))
		e = 65537
		d = inverse(e,nextprime(n)-1)
		sh.sendline(str(pow(m,d,nextprime(n))))
		sh.interactive()

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
[+] Opening connection to 04.cr.yp.toc.tf on port 37713: Done
[DEBUG] Received 0x49 bytes:
    b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n'
[DEBUG] Received 0x49 bytes:
    b'| Hello guys! This is a challenge on fault attack for signatures, our  |\n'
[DEBUG] Received 0xdb bytes:
    b"| storage can apply at most `l' bit flip-flop on signature modulus, so |\n"
    b"| try to locate the critical bits, we'll changed them to forge a sign! |\n"
    b'||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\n'
[DEBUG] Received 0x58 bytes:
    b'| Options: \n'
    b'|\t[A]pply fault \n'
    b'|\t[G]et the parameters \n'
    b'|\t[V]erify the signature \n'
    b'|\t[Q]uit\n'
[DEBUG] Sent 0x2 bytes:
    b'G\n'
[DEBUG] Received 0xc bytes:
    b'| e = 65537\n'
[DEBUG] Received 0x194 bytes:
    b'| n = 104981602711737921741067436882873969170892556169779316379641188495349180036957082719084792112570720964059438514815141682418060869265245632809444321965177466795633367170837137667604714835775110586206182696907979402763142773894052184007391308436971329481662589112186222512579266056020589656927414366334330527891\n'
    b'| Options: \n'
    b'|\t[A]pply fault \n'
    b'|\t[G]et the parameters \n'
    b'|\t[V]erify the signature \n'
    b'|\t[Q]uit\n'
[1014, 1022]
[DEBUG] Sent 0x2 bytes:
    b'A\n'
[DEBUG] Received 0x53 bytes:
    b'| please send at most 2-tuple array from indices of bits of modulus, like: 14, 313\n'
[DEBUG] Sent 0xb bytes:
    b'1014, 1022\n'
[DEBUG] Received 0x58 bytes:
    b'| Options: \n'
    b'|\t[A]pply fault \n'
    b'|\t[G]et the parameters \n'
    b'|\t[V]erify the signature \n'
    b'|\t[Q]uit\n'
[DEBUG] Sent 0x2 bytes:
    b'V\n'
[DEBUG] Received 0x24 bytes:
    b'| please send signature to verify: \n'
[DEBUG] Sent 0x135 bytes:
    b'20730183509466328767965263434529712628546542794159093618986150900322575645228000756062913760197921041709300609299520325780100786061431435079170780704339841199580838887376530568075047896696058040695642769356327691028864410997241434079700713503047076146762466890495643816679430601621097555066238145997558031723\n'
[*] Switching to interactive mode
[DEBUG] Received 0x4b bytes:
    b'| Congrats! your got the flag: CCTF{R3aLlY_tH1S_1z_Seiferts_R54_AT7aCk!!?}\n'
| Congrats! your got the flag: CCTF{R3aLlY_tH1S_1z_Seiferts_R54_AT7aCk!!?}
[*] Got EOF while reading in interactive

Mino *

分值：169

考点：-2进制？

challenge

You cannot have a good cryptosystem without mathematics! This task is an easy coding system!

1
nc 02.cr.yp.toc.tf 13771
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#!/usr/bin/env python3

import sys
from flag import flag

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Hi crypto programmers! I'm looking for some very special permutation", border)
	pr(border, "p name MINO such that sum(p(i) * (-2)^i) = 0 from 0 to n - 1, for   ", border)
	pr(border, "example for n = 6, the permutation p = (4, 2, 6, 5, 3, 1) is MINO:  ", border)
	pr(border, "4*(-2)^0 + 2*(-2)^1 + 6*(-2)^2 + 5*(-2)^3 + 3*(-2)^4 + 1*(-2)^5 = 0 ", border)
	pr(border, "In each step find such permutation and send to server, if there is  ", border)
	pr(border, "NOT such permutation for given n, just send `TINP', good luck :)    ", border)
	pr(border*72)
	step, final = 3, 40
	while True:
		pr(border, f"Send a MINO permutation of length = {step} separated by comma: ")
		p = sc().split(',')
		if step % 3 == 1:
			if p == ['TINP']:
				if step == final: die(border, f"Congrats, you got the flag: {flag}")
				else:
					pr(border, "Great, try the next level :)")
					step += 1
			else:
				die(border, "the answer is not correct, bye!!!")
		elif len(p) == step:
			try:
				p = [int(_) for _ in p]
			except:
				pr(border, "the permutation is not valid")
			if set(p) == set([_ for _ in range(1, step + 1)]):
				S = 0
				for _ in range(step):
					S += p[_] * (-2) ** _
				if S == 0:
					if step == final: 
						die(border, f"Congrats, you got the flag: {flag}")
					else:
						pr(border, "Great, try the next level :)")
						step += 1
				else:
					die(border, "the answer is not correct, bye!!!")
			else:
				pr(border, "the permutation is not valid!!!")
		else:
			die(border, f"the length of permutation is not equal to {step}")

if __name__ == "__main__":
	main()

Thought

不太会哦，用z3大力好像可以，数学的分析好像也有，等我看看

exp

https://zhuanlan.zhihu.com/p/543272688

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import z3
from pwn import remote

io = remote('02.cr.yp.toc.tf', 13771)

def rua(n):
	# 42bit的n个变量
    Q = [z3.BitVec("Q_{}".format(i), 42) for i in range(n)]
    # n个变量都大于等于1，小于等于n
    val_c = [z3.And(1 <= Q[i], Q[i] <= n) for i in range(n)]
    # n个变量都不同
    col_c = [z3.Distinct(Q)]
    # n个变量满足的关系
    con_c = [sum(Q[i] * ((-2)**i) for i in range(n)) == 0]
    solver = z3.Solver()
    solver.add(val_c + col_c + con_c)

    result = ''
    if n % 3 == 1:
        return b'TINP'
    elif solver.check() == z3.sat:
        m = solver.model()
        print("{}:".format(n), end=' ')
        for i in Q:
            result += str(m[i])
            result += ','
        return result.encode()[:-1]    # 去掉最后一个逗号
    else:
        return b'???'

for n in range(3, 40+1):
    print(io.recvuntil(b'separated by comma:'))
    result = rua(n)
    print()
    print(result)
    print()
    io.sendline(result)
    
io.interactive()
# | Congrats, you got the flag: CCTF{MINO_iZ_4N_3a5Y_Crypto_C0d!n9_T4sK!}

result

1
| Congrats, you got the flag: CCTF{MINO_iZ_4N_3a5Y_Crypto_C0d!n9_T4sK!}

Starter ECC

分值：103

考点：模 n 开根

challenge

Dive deep to the elliptic cryptosystem!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#!/usr/bin/env sage

from Crypto.Util.number import *
from secret import n, a, b, x, flag

y = bytes_to_long(flag.encode('utf-8'))

assert y < n
E = EllipticCurve(Zmod(n), [a, b])

try:
	G = E(x, y)
	print(f'x = {x}')
	print(f'a = {a}')
	print(f'b = {b}')
	print(f'n = {n}')
	print('Find the flag :P')
except:
	print('Ooops, ERROR :-(')
	
	
x = 10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046477020617917601884853827611232355455223966039590143622792803800879186033924150173912925208583
a = 31337
b = 66826418568487077181425396984743905464189470072466833884636947306507380342362386488703702812673327367379386970252278963682939080502468506452884260534949120967338532068983307061363686987539408216644249718950365322078643067666802845720939111758309026343239779555536517718292754561631504560989926785152983649035
n = 117224988229627436482659673624324558461989737163733991529810987781450160688540001366778824245275287757373389887319739241684244545745583212512813949172078079042775825145312900017512660931667853567060810331541927568102860039898116182248597291899498790518105909390331098630690977858767670061026931938152924839936
Find the flag :P

Thought

$y^2 \equiv x^3 + ax+b \pmod p$

这个 $n$ 不是素数，尝试分解

1
2
3
4
5
6
7
sage: n=117224988229627436482659673624324558461989737163733991529810987781450160
....: 68854000136677882424527528775737338988731973924168424454574558321251281394
....: 91720780790427758251453129000175126609316678535670608103315419275681028600
....: 39898116182248597291899498790518105909390331098630690977858767670061026931
....: 938152924839936
sage: print(ecm.factor(n))
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 690712633549859897233, 690712633549859897233, 690712633549859897233, 690712633549859897233, 690712633549859897233, 690712633549859897233, 651132262883189171676209466993073, 651132262883189171676209466993073, 651132262883189171676209466993073, 651132262883189171676209466993073, 651132262883189171676209466993073]

exp

https://zhuanlan.zhihu.com/p/543272688

1
2
3
4
5
6
7
8
9
10
11
12
13
14
q1 = 2^63
q2 = 690712633549859897233 ^ 6
q3 = 651132262883189171676209466993073 ^ 5
G1s = Mod(x ** 3 + a * x + b, q1).nth_root(2, all=True)
G2s = Mod(x ** 3 + a * x + b, q2).nth_root(2, all=True)
G3s = Mod(x ** 3 + a * x + b, q3).nth_root(2, all=True)

for G1 in G1s:
    for G2 in G2s:
        for G3 in G3s:
            m = long_to_bytes(int(crt([ZZ(G1), ZZ(G2), ZZ(G3)], [q1, q2, q3])))
                if b'CCTF{' in m:
                    print(m)
                    break

result

1
b' CCTF{8E4uTy_0f_L1f7iN9_cOm3_Up!!}  CCTF{8E4uTy_0f_L1f7iN9_cOm3_Up!!}  CCTF{8E4uTy_0f_L1f7iN9_cOm3_Up!!} _______________________'

medium-hard

Watery soup

分值：226

考点：构造

challenge

Watery soup

Find a message in a mess!

1
nc 05.cr.yp.toc.tf 37377
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#!/usr/bin/env python3

from Crypto.Util.number import *
import sys
#from flag import flag

flag = bytes_to_long(b"a"*33)
assert 256 < flag.bit_length() < 512

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc(): return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Hi crypto-experts, send us your prime and we will mix the flag with ", border)
	pr(border, "it! Now can you find the flag in the mixed watery soup!? Good luck! ", border)
	pr(border*72)
	while True:
		pr("| Options: \n|\t[S]end the prime! \n|\t[Q]uit")
		ans = sc().lower()
		if ans == 's':
			pr(border, "Send your prime here: ")
			p = sc()
			try: p = int(p)
			except: die(border, "Your input is not valid!!")
			if not (128 <= p.bit_length() <= 224): die(border, "Your prime is out of bounds :(")
			if not isPrime(p): die(border, "Your input is NOT prime! Kidding me!?")
			pr(border, "Send the base here: ")
			g = sc()
			try: g = int(g) % p
			except: die("| Your base is not valid!!")
			if not (64 < g.bit_length() < 128): die(border, "Your base is too small!!")
			result = (pow(g ** 3 * flag, flag - g, p) * flag + flag * flag + g) % p
			pr(border, f"WooW, here is the mixed flag: {result}")
		elif ans == 'q': die(border, "Quitting ...")
		else: die(border, "Bye ...")

if __name__ == '__main__': main()

Thought

$O(g) = (g^3 \cdot f) ^ {f-g} \cdot f + f^2 + g \pmod p$

如果直接解方程得话，因为 $f-g$ 不知道。所以想着能不能联立方程把这 $f$ 消掉。然后想着能不能找到两个 $g$，满足 $g_i^3 \equiv 1 \pmod p$ ，然后就有
$$
(O(g_1)-f^2-g_1)/(O(g_2)-f^2-g_2) \equiv (f^{f-g_1}f) / (f^{f-g_2}f) \equiv f^{g_2-g_1} \pmod p \
(O(g_1)-f^2-g_1) \equiv f^{g_2-g_1} \cdot (O(g_2)-f^2-g_2) \pmod p \
(O(g_1)-f^2-g_1) - f^{g_2-g_1} \cdot (O(g_2)-f^2-g_2) \equiv 0 \pmod p
$$
但是这个degree $(g_2-g_1)$ 太大了，如果控制 $g_2-g_1$ 的值
$$
(O(g_1)-f^2-g_1)/(O(g_2)-f^2-g_2) \equiv (g_1^{3f-3g_1}f^{f-g_1}f) / (g_2^{3f-3g_2}f^{f-g_2}f) \equiv (\frac{g_2^{3f-3g_2}}{g_1^{3f-3g_1}})f^{g_2-g_1} \pmod p \
$$
右式前面那一大块还是有 $f$，

除法不行再来看看乘法，因为有负幂次

如果 $(O(g_1)-f^2-g_1) \cdot (O(g_2) -f^2-g_2) \equiv (g_1^3 \cdot f)^{f-g_1} \cdot f \cdot (g_2^3 \cdot f)^{f-g_2} \cdot f \equiv (g_1g_2)^{3f}/g_1^{3g_1}g_2^{3g_2} \cdot f^{f+1} \cdot f^{f+1} / f^{g_1+g_2} $

这里能不能控制 $g_1g_2=\pm 1,g_1+g_2 = 0$，但是要求 $64\lt g.nbits() \lt 128$，而且还有一个 $f^{2f+2}$ 呢。

如果要处理掉那个 $f^{2f+2}$ ，我们可以给两个交互的值做一个幂次，即原式改为
$$
(O(g_1)-f^2-g_1)^X \cdot (O(g_2) -f^2-g_2)^Y \equiv (g_1^Xg_2^Y)^{3f}/g_1^{3g_1X}g_2^{3g_2Y} \cdot f^{X(f+1)+Y(f+1)} / f^{g_1X+g_2Y}
$$
那就考虑 $g_1^Xg_2^Y=1,g_1X+g_2Y=0,X+Y=0$

显然这里要求$X=-Y$，那就需要 $g_1=g_2=1$ 了，不太行

那我们就再加一条变量
$$
g_1^Xg_2^Yg_3^Z=1,g_1X+g_2Y+g_3Z=0,X+Y+Z=0
$$

姑且设 $X=Y=1,Z=-2$

就有 $g_1g_2 \equiv g_3^2,g_1+g_2\equiv2g_3$

似乎只有 $g_1=g_2=g_3$ 才能满足这些条件，但这显然不符合题目要求。

我们再设 $X=1,Y=2,Z=-3$

就有 $g_1g_2^2\equiv g_3^3,g_1+2g_2\equiv 3g_3$

我们有 $g_1 =-8g_2 ,g_3 = -2g_2$

然后我们就有
$$
(O(g_1)-f^2-g_1)^1 \cdot (O(g_2) -f^2-g_2)^2\cdot(O(g_3) -f^2-g_3)^{-3} \equiv (g_1^Xg_2^Yg_3^Z)^{3f}/g_1^{3Xg_1}g_2^{3Yg_2}g_3^{-3Zg_3} \cdot f^{(f+1)(1+2-3)} / f^{g_1X+g_2Y+g3Z} \ \equiv 1/g_1^{3g_1}g_2^{6g_2}g_3^{-9g_3} / f^{g_1X+g_2Y+g3Z}
$$
注意到这里是 $g_1X+g_2Y+g_3Z \equiv 0 \pmod p$，实际上 $3p-8g_2 + 2g_2+ -6g_2+-3p = 0$ 所以上式右手边为
$$
1/g_1^{3g_1}g_2^{6g_2}g_3^{-9g_3}
$$
所以
$$
(O(g_1)-f^2-g_1)^1 \cdot (O(g_2) -f^2-g_2)^2 \cdot g_1^{3g_1}g_2^{6g_2}g_3^{-9g_3} =(O(g_3) -f^2-g_3)^{3}
$$
PS：这里用的前面的脚本找的 $p-1$ 光滑的 $p$，也不知道有没有必要就是说（因为前面有求离散对数的想法…..）

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#!/usr/bin/env python3

from Crypto.Util.number import *


def gen_primes(nbit, imbalance):
	p = 2
	FACTORS = [p]
	while p.bit_length() < nbit - 2 * imbalance:
		factor = getPrime(imbalance)
		FACTORS.append(factor)
		p *= factor
	rbit = (nbit - p.bit_length()) // 2

	while True:
		r, s = [getPrime(rbit) for _ in '01']
		_p = p * r * s
		if _p.bit_length() < nbit: rbit += 1
		if _p.bit_length() > nbit: rbit -= 1
		if isPrime(_p + 1):
			FACTORS.extend((r, s))
			p = _p + 1
			break

	FACTORS.sort()
	return (p, FACTORS)

def genkey(nbit, imbalance, e):
	while True:
		p, FACTORS = gen_primes(nbit // 2, imbalance)
		if len(FACTORS) != len(set(FACTORS)):
			continue
		q, q_factors = gen_primes(nbit // 2, imbalance + 1)
		if len(q_factors) != len(set(q_factors)):
			continue
		factors = FACTORS + q_factors
		if e not in factors:
			break
	print(p.bit_length(),q.bit_length())
	n = p * q
	return n, (p, q)

nbit = 256
imbalance = 16
e = 0x10001


n, PRIMES = genkey(nbit, imbalance, e)
print(PRIMES)

p = 241073702737973665011723294586981868543
p = 281001512981116565134944031254704290547
p = 243080850308481335113421227369194998483
p = 269995126298881109995199221021359578159
g2 = 2**126
g1 =  (-8 * g2)%p
g3 = (-2 * g2)%p


print(p.bit_length(),g1.bit_length(),g2.bit_length(),g3.bit_length())

# sage
from pwn import *
context.log_level='debug'
sh = remote("05.cr.yp.toc.tf",37377)
def oracle(g,p):
	sh.recvuntil("[Q]uit\n")
	sh.sendline("S")
	sh.recvuntil("here: \n")
	sh.sendline(str(p))
	sh.recvuntil("here: \n")
	sh.sendline(str(g))
	sh.recvuntil("flag: ")
	return int(sh.recvuntil("\n")[:-1])

ps = [241073702737973665011723294586981868543,
281001512981116565134944031254704290547,
243080850308481335113421227369194998483,
269995126298881109995199221021359578159]
mp=[]
for p in ps:
	g2 = 2**126
	c2=oracle(g2,p)
	g1 =  (-8 * g2)%p
	c1=oracle(g1,p)
	g3 = (-2 * g2)%p
	c3=oracle(g3,p)

	#print(p.bit_length(),g1.bit_length(),g2.bit_length(),g3.bit_length())
	R.<x> = Zmod(p)[]
	z1 = pow(g1,3*g1,p)
	z2 = pow(g2,6*g2,p)
	z3 = pow(g3,-9*g3,p)
	f = (c1-x^2-g1)*((c2-x^2-g2)^2)*z1*z2*z3 - (c3-x^2-g3)^3
	mp.append([f.roots()[i][0] for i in range(2)])

from Crypto.Util.number import *
for i in mp[0]:
	for j in mp[1]:
		for k in mp[2]:
			for l in mp[3]:
				m = crt([int(i),int(j),int(k),int(l)],ps)
				if b"CCTF" in long_to_bytes(m):
					print(long_to_bytes(m))

result

1
b'CCTF{Pl34se_S!r_i_w4N7_5omE_M0R3_5OuP!!}'

313 Loyal

分值：209

考点：paillier cryptosystem, Homomorphic properties

challenge

I have developed a probabilistic asymmetric algorithm for public key cryptography. Then I added some functions to harden it, you can try this oracle now. But I think it is still unbreakable! What about you?

Note: The source code updated, please download again!

1
nc 07.cr.yp.toc.tf 31377

Thought

同态走一波，交互中的处理解密后相当于

$m_i = r\cdot (D(poly[0]) \cdot f_i + D(poly[1]) \cdot f_i^2 + D(poly[2]) \cdot f_i^3 \cdots) + f_i$

poly给个 $[E(0),E(0)]$，然后解密就能直接得到明文 y4HCcRRMt{h!PF_00nOT71e3o3N0RCn_C5}pmH_C3!M

被最后 shuffle(result) 了，所以我们得构造一下，留一个标志

23333，不用了就是说，题目有POINTS.sort()，

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
#!/usr/bin/env python3

from Crypto.Util.number import *
from random import *
import sys
flag= b"a"*2

def keygen(nbit):
	p, q = [getPrime(nbit) for _ in '__']
	n, phi = p * q, (p - 1) * (q - 1) // 2
	while True:
		g = getRandomRange(2, n ** 2)
		if GCD(g, n) == 1:
			w = (pow(g, phi, n ** 2) - 1) // n
			if GCD(w, n) == 1:
				u = inverse(w, n)
				break
	pkey, skey = (n, g), (phi, u)
	return pkey, skey

def encrypt(pkey, m):
	n, g = pkey
	while True:
		r = getRandomRange(2, n)
		if GCD(r, n) == 1:
			break
	return (pow(g, m, n ** 2) * pow(r, n, n ** 2)) % (n ** 2)

def L(x,n):
	return (x-1)//n

def decrypt(sk,c,n):
	Lambda, u = sk
	m=(L(pow(c,Lambda,n**2),n)*u)%n
	return m

def add(pkey, a, b):
	n, g = pkey
	return pow(a * b, 1, n ** 2)

def multiply(pkey, a, k):
	n, g = pkey
	return pow(a, k, n ** 2)

def mul_poly(n, P, Q):
	R = [0] * (len(P) + len(Q))
	for i in range(len(P)):
		for j in range(len(Q)):
			R[i+j] += (R[i + j] + P[i] * Q[j]) % n
	return R

def encrypt_poly(pkey, poly):
	return [encrypt(pkey, term) for term in poly]

def client_genpoly(pkey, points):
	n, g = pkey
	result = [1]
	for point in points:
		result = mul_poly(n, result, [-point, 1])
	return encrypt_poly(pkey, result)

def evaluate_poly(pkey, poly, point):
	n, g = pkey
	_point = point
	result = poly[0]
	for term in poly[1:]:
		result = add((n, g), result, multiply((n, g), term, _point))
		_point = (_point * point) % n
	return result

def backend(pkey, poly, points):
	n, g = pkey
	R = []
	for point in points:
		result = evaluate_poly((n, g), poly, point)
		result = multiply((n, g), result, getRandomRange(2, n))
		result = add((n, g), result, encrypt((n, g), point))
		R.append(result)
	return R

POINTS = []
for i in range(len(flag)):
	POINTS.append(getRandomRange(2, 2 ** 64) * 2 ** 10)
POINTS.sort()
for i in range(len(flag)):
	POINTS[i] += flag[i]

nbit = 256

#pkey, skey = keygen(nbit)
pkey,skey = (8983025019747376462297416653504653560143717774277487268850273211947558329216360360860149180983608842607976796458487804140587479094830448025755096545144497, 39731172096476404258382334612980796427609232314781624939316778468164398684304697816364082061332364391985762624841996838368191881107968535717464420001080645817166058541017585108878564010798647594217487978324909939331031718886070579425358413244493346052109748996979570687086012138664475326345367218468552512086),(4491512509873688231148708326752326780071858887138743634425136605973779164608084844589301889169145935681436639346715428462044150156908234212259061733932920, 4133856416919793681590686025820765995031321904145976790655198178331831628277063442563440913562455923032491945677717658580173062624722204381499487375119933)


poly=[encrypt(pkey, 0),encrypt(pkey, 0)]
n, g = pkey

print(n,g,poly)

sss='''| result[0] = 60701364673871368538672568836694311974506205703702029549362893423258772988050577833644429122896297207330382559025081100751629571179362400300526188189076137343111793106728012955599396780803405599378051881052727474682664697093677194443957613411615172000197331483387389884778856023319785421334200063270381794245
| result[1] = 54505714023959132539972540688273793053755576505190909700054456607838006099291584770540537730243507874746681470857190139174290757042575260752923724728528845611068152921759850791799612575694366614271035784244451561577073442533475082357578907456819057436882288500053622940420064191767820086387187184772178256497
| result[2] = 31482244269832774302093219880499960291092953288614981664817704153996471648027597538939919368674593181731850603888742067705595887769325167576209320201407316156336137340227336618516467329067898696235846119526980514739643514081826011063177630375473132122049959095866560734181203259240441268829305730268427579685
| result[3] = 21269066534820844791903168351253302661378009045674764390133221391276174842373822387597405434628556894312217790806291276037409254287468293050701198484505770521595433289369839519721579595787060878774858828606500407079695185066234462690263778600053319024374276255764488142419865011778652942825456439614530036182
| result[4] = 17726688771976154885068730043455190883269525441213807838865038191027099148933756456549504383830879493031235136629811919521296600120227451862950706601942977884966702073741341153318302017722743040836247425707534542820001264527443892457287555950173184850226884844739032122047194624286155254268875821400430386321
| result[5] = 35581860655885092163483423400346604048689462882882756754696573796856489300986953276945441662627908812024483199273448987644659097506243719064998224363682189335983202107500032263863291681096106130637052651193832633671948091747294161464258463889308647962824508327390390650679389972240071848285431037044105552233
| result[6] = 70262218169601168956325601146922998952758183545527211453224197174981655643641099966205886141855918596111593666554717771410172939175497105544879908243706049912133917567731452132168722472538476463808992582205023905085397231349624852553455711496951840895898245143454512962517257059736155462811528287491960222811
| result[7] = 12795117201194967356790541767668503114512267924019154453299343963799658595350519091984396355283867471414940033580848375556021804326920619318336061567977170749771351426069410874784474080666633610622194644115206647671405511436907963852061379452634326650130519927260404794281102388305192155249980768944441280471
| result[8] = 29614433752881257272277719367139685519484335743547386264168479475287866599885672429175204283879232251961892489046631280581012707224071363004503873402293012268519245078765587356381014458209571551725872928819409282901936309811795817960029002685763790797353218312562241768989927598431689513275239472807021572121
| result[9] = 22516684635991635065182175951574008748645594707696075503632060278079922388870212564838708853941193363162655002517327432839511180511583812509070476724216895559593653276325046380499276877625735383199723596826765590155361573577165401043883039817755746315963588141798754540600102754781847194135018739913349584325
| result[10] = 1339945017160788466449485665736181293162591496361869736683106272175197140314512332067400900882128298356853178709406745208489487324155606987895628957051620054237283981565019443455134181725526400014921850478169026122185673232067346596544798652729165373964320102330730067233005556496906482453865684099988479342
| result[11] = 69287254090604496674918155397472179581957432096162716627815636171887889809467590691268907858811035260195401500095282594042326418234802296422699163230836030885597935514069001789428122963439563661308573241468388769427582928754923242908307990506355393534001812279916307461414259500536345485791099863372329968516
| result[12] = 16759195422769792610127771210117391726944171091960737436816027260267361242568176831615850689545674228431077479440113492402670084544913473934877885900484018440139750880875692736494521041184954785268325445749973975236495533868121750798206380377508248400505013953093455091827903321761208544245394309774591546395
| result[13] = 40076475379029371315691157200374026961747171058330824061101835445496727092845629664524783040634705720942455820068625166283109353526947365834814723045977897185871358640938536741635051089728423626703553081232221444893658041997500816069252829805377769851132893495601067711546657375590586972401185000811090538556
| result[14] = 71711004763431424129547279193776888780357334638452565649002027919142044843666680509948122126885305221812382045508159337933772320896035393540028929112525682443519842260052075295474113780344796225664867487894619980383279601210802426421659731479120671643141277657873408560107161345390192707512858287529651245448
| result[15] = 20791606033656016094628617966269089226353549652775886836019052383791942426855144814747295577757921371976866164329349645609464972383827102785335688127856988493675064136357879213697810232281168602926111102710825913940354102696646943460488018001635217090248096358971800532491872474089547217755862145072867276542
| result[16] = 75524796633982208988704715912551473165739274261376865710511985564725927093621311103209006337490642009376977419432905758229967199550227182286550063329853621598567020160251853455880998695700660919497831080903697828163730364557176458905625438052775129018222117239901453595778508046235381339138007336966032324535
| result[17] = 8821813905989979131671277386728618272145461865669972320058426591083853774477907837111890468040625018780557786597007447873957277103650906996194158170295426494039135922277187270313428972125836953999732388034444009264401164058693978746681473885803480822682058162436082477237896733586941813822379944063916878697
| result[18] = 23858579030504548241394613331295867198916269460872458465558167844852843524509093805961758176046984464107174210993292230359775865831814447038056030806145659606453953040642384946279969215189118913421400189708886415836423398229662028407376356069183805193076648017540211920742826759333101825692605013711191136020
| result[19] = 934691835420305526483841120251772815643874087754271794308790330077781534745150901189607930781692409677029622226345023293229542700197995990260735788372365951153923507008089479231807432435175850743569091091473668227829899512073056579351296104763407053907440608295772379945533040961249797778027187386892577409
| result[20] = 53549326491556749245124248564268528821304323571880706981893457503747477811102312751500086148327418003669244023202262176169698430461986240040349438290533272977313096142506488063219805928857426817401427953360725210678433115875094005559608578659535326221442286819812159815477568142048732876412309634036656163383
| result[21] = 55222350252509841239140906398549112453023112784051423474488231284008422771804656845898906882092803323934840505694907034823428039348059313701490198494447012089972533698980894869449739174355919506421462980119002317262647649678822486909740793069625376401214410464118657618576751705231517657112923330480129163394
| result[22] = 54383042832687713152567981432614245327630896037469221404407886398271140627907017215225774516223165346359927709989294147500632532772555538685927915311322506185391512320849008655889439012410485535733412422971914444079238718453454722882305550858527415261592835787831733420514341201076280150947118345123209496012
| result[23] = 35415702116663719793679309448571441230335649679652346834210419087350802031133309520073015911063285528629022024352907476161782855987076300661107679853841683814773684984169614895405277661201978429338749283770763851935118478987027774273704012395378393392542417614803751239822859680337021232315288108113937955559
| result[24] = 77311376414735233091956925933342928635274708978684257645716804113399553714023582531606632148219973368218663671818272949206705169102858209221722695656667309363292271658133480258326067427799155774927621719945542178413438011676663469293983659580695729373384539727292051117574982243216380519888106880694068805459
| result[25] = 41529714518679104456615099430616845758081983056782336280293129613853047748833367214325002402088267190715021804748920865648623142120762365373486732842097196455013020239183373288560579426060067065200687134951220591419796173683082768759178244260749561617826924419724965737951294141815332259905076567273380342177
| result[26] = 78934023973015547410359494363011141527469488211362978027088562576806145819907602342663202811386262957958206387482929933988164037938470659762979908216223301192758348367718269596157629223033973655947043016564897417294289237275113109491408825385592653262318324018451966103321399494158210669053321466011572476847
| result[27] = 31320932316349772286090465232054051051794176405615427761015386696879261190809549392813975028528244110973110290836076211124423336616805929661320599863336097529328581211163055065734185337408202198281433156367205004278804400721515226117011598135605514325123860975124167724734310634078420797712784387943565985110
| result[28] = 61615833676933166082336769086865871102842316919223122542627395419340729976208316064129377840521633914555726016159708596002280745351159091674638816460543183975329476881154656750277826741549021923954431146823964960957247463417286875159841420162547932323979806824067555767117476865553844067525850274474528310300
| result[29] = 17858697213202683161095184745886187415275787380085552763742038120241448556523577559354574407298939206384922615872921969122001896758816300114206424258775064641472200311508468415911230460642933946709514830211212437819850220045660751502932617516023512439140337808639567904890680530997742980734415435491937931896
| result[30] = 3434679003838847163230386258508564509713009872010917063071366577777488194486755137625580191263544013040811511414866060499420987984928091739783507148430519983183462340816454466818030316353979327963586666864800323464320201740717379130520629294212475880348101143712755093953200931878487537101552012773370045627
| result[31] = 55296486580580674560805022792730615650519578766688949252371702762297452719999098301631097181290431080042142914125893404202623920417018513557281534022989920235187922354988868589310212321921390540431679801324448103623007589571658233073651712640016981974799501707571209596837130813154256991941292070451355395380
| result[32] = 15683825059527223744056559682501511982536292418609203084237839963457310068132683264168727671275680302490244705634262449947105833465996329110361763861608163199981669075229559205476635001650097328661633243706699479067393531345965482175515036427994577377274992050348435132143535739363139813580800713500429127065
| result[33] = 79089731655664659421603701833691817423495974527897708959327431353455727425456568751635923281066657148662633492890002349386988937076599708551229475839546853604231487216737963865879551273025826861120723430354740649623843510117035933223660569937381004632700211522998544177138130673468395371318985629073789065357
| result[34] = 21460569824913655171261677385370818404934528843151111628075679981669110572059639575626981528972048815714209025453761968527275361557400560847301343810003625153454672557464316157235901370027950440322810565935022120998393518027122731289398755638997871869907101597359826962558902864673989372721016666049925650456
| result[35] = 30357471700897552827588297838542720645386484333478129105962277235466808483733870098842125393221161608048289152018209708501847369893338903483565136799865265174008363276636836194733392700986172931337953060989654862206958291624691265415920595603184924445235289465285373366794324067611598749426104313055248956579
| result[36] = 66195583187466117471431580178815062033164755151649992899793859026634080016710366841208725185551306734328472884653610803182778870799901014792670791103922055538575835052024690253183215321298262572403313762043049029002001953084713647685627055829424534242613423062212897992476762005673257095764681970896250671977
| result[37] = 49003911875690116658875014605984263634059650654319648994446147615046601855298150424169467393711635423011526567537856233200950969219779755961991090713065462433404962543490156490003111216311825890057037851527298511148357386169299834738232886428272502312162237066368599033590454216553600861428053516351207797738
| result[38] = 71367507491803672303364505077824359178753951125198410885479851268132353311554430864849726439584142081399817020973667387514217321690324236692494737176377601896066101227401121377079365052095828656895214799717485621919836974687118767825265878571278372393160561486223736309187425009160566974812123118299140384922
| result[39] = 62810724118805848993600135122928217303463453389592498155023439284527208066517510405001857312033709938339306862351827643950609861193914434015030848271112503738231025359385022570295192906772755510341170000274076201885965220443563737035555070984218612183175594820652181581289717135252336955223668490546941035537
| result[40] = 5585457931032915832452313196463091909937038840006585046682204809222004352562452949273528731683581615387381285540890461310330004452940347866062260003436613153190062784622122799496024876466499050538011049727193114822050841701337547804987309371247881052842796308870640486783600153729825434741583060065857691505
| result[41] = 4551901454601621574045444424560231904405727779309037751700646898796048961418144067884934876185646894270404401223262702541764467186770568803615731121737754164145010313690402193230027097096584685203156659860239857995081847694616569736058642643088485789477439723117576747922343102011800468997460503802299169159
| result[42] = 15231283044446661621363810174458377379980965061715034718556694049908017350322106494968359959811085843236362313017612200292407984558138898897354872227653574153128944365979225025175276492473114296217737767152406059316217564256938742314016275744469500854371658586413444573112320110206311867383041609094690184151
'''
import re
s = re.findall(".*? = (\d+)",sss)
#print(s)
flag=""
FLAG = []
for each in s:
	FLAG += [decrypt(skey,int(each),n)]
FLAG.sort()
flag = ''.join(chr(i%256) for i in FLAG)
print(flag)

result

1
CCTF{4n0t3R_h0MomORpH1C_3NcRyP7!0n_5CH3Me!}

Soda*

分值：209

考点：signature forge

challenge

You may ask yourself how factoreal is skipping RSA? Here he comes with this one!

1
nc 01.cr.yp.toc.tf 37711
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#!/usr/bin/env python3

from Crypto.Util.number import *
import sys
from secret import p, q, flag

def soda(g, p, q, m):
	n, phi = p * q, (p - 1) * (q - 1)
	if isPrime(m) and m.bit_length() <= 128:
		e = m
	else:
		e = 2 * (pow(g, m**2, n) % 2**152) ^ 1
	if GCD(e, phi) == 1:
		d = inverse(e, phi)
		return pow(g, d, n)

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Hi all cryptographers! Welcome to SODA crypto oracle, we do SODAing!", border)
	pr(border, "You mission is find a way to SODA a given message, I think its easy.", border)
	border = "|"
	
	n = p * q
	phi = (p - 1) * (q - 1)
	g = 31337

	CRY = "Long Live Crypto :))"
	m = bytes_to_long(CRY.encode('utf-8'))

	while True:
		pr("| Options: \n|\t[G]et the parameters \n|\t[T]ry the soda \n|\t[V]erify the signature \n|\t[Q]uit")
		ans = sc().lower()

		if ans == 'g':
			pr(border, f'n = {n}')
			pr(border, f'g = {g}')
		elif ans == 't':
			pr(border, "please send your integer to get soda: ")
			s = sc()
			try:
				s = int(s)
			except:
				die(border, "Something went wrong! Your input is not valid!! Bye!!!")
			h = soda(g, p, q, s)
			if h != None:
				if s == m:
					die(border, 'Are you kidding me? We will never SODA it!! Bye!!!')
				else:
					pr(border, f"soda(g, p, q, m) = {soda(g, p, q, s)}")
			else:
				pr(border, 'Something went wrong! See source code!!')	
		elif ans == "v":
			pr(border, "please send the soda to verify: ")
			sd = sc()
			try:
				sd = int(sd)
			except:
				die(border, "Your input is not valid! Bye!!")
			_e = 2 * (pow(g, m**2, n) % 2**152) ^ 1
			if pow(sd, _e, n) == g:
				die(border, "Congrats! your got the flag: " + flag)
			else:
				pr(border, "[ERR]: Your answer is NOT correct!!!")
		elif ans == 'q':
			die(border, "Quitting ...")
		else:
			die(border, "Bye bye ...")

if __name__ == "__main__":
	main()

Thought

$e = 2 \cdot (g^{m^2}%n) % 2^{152}) \oplus 1$

这里用的是 $m^2$

限制不让 $s=m$

emmmm，但是没说不让 $s=-m$

exp

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
[root@VM-0-7-centos ~]# nc 01.cr.yp.toc.tf 37711
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hi all cryptographers! Welcome to SODA crypto oracle, we do SODAing! |
| You mission is find a way to SODA a given message, I think its easy. |
| Options: 
|	[G]et the parameters 
|	[T]ry the soda 
|	[V]erify the signature 
|	[Q]uit
T
| please send your integer to get soda: 
-436368298743117038953816769867134146642565540137
| soda(g, p, q, m) = 79559095642922266463148997031064319613325134865931925211002769523336997914218584554135332631438918297442868689016949177146172826664238399782606128281653170770356172139616842694434150846482170779338124730300765599381100281978959304884291887782907002310338483665832672081733896484850235842710260881749486555655
| Options: 
|	[G]et the parameters 
|	[T]ry the soda 
|	[V]erify the signature 
|	[Q]uit
V
| please send the soda to verify: 
79559095642922266463148997031064319613325134865931925211002769523336997914218584554135332631438918297442868689016949177146172826664238399782606128281653170770356172139616842694434150846482170779338124730300765599381100281978959304884291887782907002310338483665832672081733896484850235842710260881749486555655
| Congrats! your got the flag: CCTF{f4cToriZat!On__5Tt4cK_0n_4_5i9na7urE!}

Sparse*

分值：114

考点：RSA

challenge

RSA is fun, the frozen RSA is even more fun!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

def sparse(p, k):
	nbit = p.bit_length()
	while True:
		CF = [getRandomRange(-1, 1) for _ in '_' * k]
		XP = [getRandomRange(3, nbit - 3) for _ in '_' * k]
		A = sum([CF[_] * 2 ** XP[_] for _ in range(0, k)])
		q = p + A
		if isPrime(q) * A != 0:
			return q

p = getPrime(417)
q = sparse(p, 5)
e, n = 65537, p * q
print(f'n = {n}')
m = bytes_to_long(flag.encode('utf-8'))
assert m < n
c = pow(m, e, n)
print(f'c = {c}')

n = 94144887513744538681657844856583985690903055376400570170371837200724227314957348031684706936655253125445176582486308241015430205703156336248578475428712275706238423997982248462635972817633320331030484841129628650918661036694615254018290264619628335177
c = 80250313885079761377138486357617323555591919111371649902793873860183455237161293320577683249054725852540874552433031133240624696119120378419135912301004715004977978507247634217071922495893934816945961054193052791946557226599493364850793396744903765857

Thought

$p,q$ 有小于十个不同的比特。

（由于题目的p,q仅有一个比特不同，所以很容易遍历，但是如果有10个比特不同，很难想象，应该有别的方法）

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
import gmpy2
n = 94144887513744538681657844856583985690903055376400570170371837200724227314957348031684706936655253125445176582486308241015430205703156336248578475428712275706238423997982248462635972817633320331030484841129628650918661036694615254018290264619628335177
c = 80250313885079761377138486357617323555591919111371649902793873860183455237161293320577683249054725852540874552433031133240624696119120378419135912301004715004977978507247634217071922495893934816945961054193052791946557226599493364850793396744903765857
list1=[]
for i in range(3,417-3):
    list1.append(2**i)
for a in list1:
    A = a
    z = gmpy2.iroot(A**2+4*n,2)
    if z[1]:
        if isPrime((A+z[0])//2):
            p = ((A+z[0])//2)
            q = n//p
            e = 65537
            d = inverse(e,(p-1)*(q-1))
            m = pow(c,d,n)
            print(long_to_bytes(m))

result

1
b'CCTF{5pArs3_dIfFeRenc3_f4ct0r1za7iOn_m3th0d!}'

Larisa

分值：174

考点：SymmetricGroup

challenge

You think you can understand the way our cryptosystem encrypts messages? Here you can challenge yourself by decrypting this message!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#!/usr/bin/env sage

from flag import flag

def genperm(n):
	_ = list(range(1, n + 1))
	shuffle(_)
	return _

def genlatrow(n):
	A = []
	for _ in range(n): A.append(genperm(n))
	return A

def prodlat(A, B):
	assert len(A) == len(B)
	C, G = [], SymmetricGroup(len(A))
	for _ in range(len(A)):
		g = (G(A[_]) * G(B[_])).tuple()
		C.append(list(g))
	return C

def powlat(A, n):
	assert n >= 0
	B = bin(n)[2:]
	c, R = len(B), [list(range(1, len(A) + 1)) for _ in range(len(A))]
	if n == 0: return R
	else:	
		for b in B:
			if b == '1':
				if c == 1: R = prodlat(R, A)
				else:
					T = A
					for _ in range(c - 1): T = prodlat(T, T)
					R = prodlat(R, T)
			c -= 1
	return R

def pad(msg, n):
	assert len(msg) <= n
	return msg + msg[-1] * (n - len(msg))

def embed(msg, n):
	assert len(msg) < n
	msg = pad(msg, n)
	while True:
		r, s = [randint(2, n) for _ in '__']
		if gcd(r, len(msg)) == 1:
			break
	A = []
	for _ in range(n):
		while True:
			R = genperm(n)
			if R[(_ * r + s) % n] == ord(msg[_]):
				A.append(R)
				break
	return A

def encrypt(A, e = 65537):
	return powlat(A, e)

l, e = 128, 65537
M = embed(flag, l)
C = encrypt(M, e)
print(C)

Thought

组了一个多维的SymmetricGroup，然后实现了一下幂运算。用的最经典的那个平方乘方法

并不能把他看作是一个矩阵，，因为做幂次运算的时候，每一行都仅与自己相关，所以在做幂次运算的时候，其实也可以给他拆开来一行一行做

1
2
3
4
5
6
7
def prodlat(A, B):
    assert len(A) == len(B)
    C, G = [], SymmetricGroup(len(A))
    for _ in range(len(A)):
        g = (G(A[_]) * G(B[_])).tuple()
        C.append(list(g))
    return C

加密是$C = M^e$，我们可以拿到阶，计算一下逆元，再乘回来就好了

exp

https://remyoudompheng.github.io/ctf/cryptoctf2022/larisa.html

1
2
3
4
5
6
7
8
9
10
11
12
13
14
t = [[...]]
embed = []
G = SymmetricGroup(128)
for perm in t:
    g = G(perm)
    order = g.order()
    d = pow(65537, -1, order)
    embed.append((g**d).tuple())

for r in range(1, 128, 2):
    for s in range(128):
        txt = bytes(embed[i][(r * i + s) % 128] for i in range(128))
        if b"CCTF" in txt:
            print(txt)

result

1
b'the flag: CCTF{pUbliC_k3y_crypt0graphY_u5in9_rOw-l4t!N_5quAr3S!}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}'

Shaim

分值：226

考点：分组哈希

challenge

1
2
3
Do you believe that every hash function has weaknesses? If yes, can you find any collision?

nc 01.cr.yp.toc.tf 37113

Thought

$h1 = msg+length+padding$

$h2 = Sbox(h1)$

$H_0 = h2[0]$

$H_i = E(H_{i-1}) \oplus H_{i-1} \oplus h2_i$

$hash = sha256(H_{-1})$

想要哈希一样的话，我们其实只用管最后一组就好，不过最后一组是length+padding或者纯padding，我们不能随意控制。

换个想法，由于后一组的结果与前一组相关，我们也可以控制前面的值，让其到达后面的值与原值一致即可。

考虑前三组，

$H_0 = h2_0$

$H_1 = E(H_{0}) \oplus H_{0} \oplus h2_1$

$H_2 = E(H_{1}) \oplus H_{1} \oplus h2_2$

我们只要更改 $h2_0,h2_1$ 为 $$h2_0’,h2_1’$$，使得后面的 $H_1’ = H_1$ ，这样后面也就都有 $H_i’ = H_i$ 即可满足条件。

若改为 $h2_0’$，那么 $H_1’ = E(H_0’) \oplus H_0’ \oplus h2_1$

想要让 $H_1’ = H_1$

可以两边同时异或 $H_1’ \oplus H_1$

则有 $H_1 = E(H_0’) \oplus H_0’ \oplus h2_1 \oplus H_1’ \oplus H_1$

于是我们设 $h2_1’ = h2_1 \oplus H_1’ \oplus H_1$

不过就是说，想要走到 $h2$，还得过一个 $Sbox$，所以我们控制 $h2$ 的话，得先逆一个 $Sbox$ 去控制 $msg$，然后题目很恶心的用了 $utf-8$，就没那么随心所欲了。需要en爆。这里我们每次随机控制 $msg_1$，然后计算 $msg_2$，遇到符合要求的，就传过去。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
from Crypto.Util.number import *
from Crypto.Cipher import DES
from hashlib import sha256
import sys, string

def randstr(l):
	rstr = [(string.printable[:62] + '_')[getRandomRange(0, 62)] for _ in range(l)]
	return ''.join(rstr).encode('utf-8')

def shaim(msg):
	SBOX = [
		0xbe, 0xc5, 0x0f, 0x83, 0xb2, 0x77, 0xa8, 0x40, 0x4c, 0x53, 0x65, 0xd6, 0x27, 0xa7, 0x7c, 0x48, 
		0x1a, 0x60, 0x30, 0x17, 0xf3, 0x80, 0x04, 0x74, 0xd2, 0x5a, 0x2c, 0x8e, 0xa0, 0x32, 0x38, 0xcb, 
		0xe5, 0x4d, 0x19, 0x8f, 0xd9, 0x6d, 0x86, 0x58, 0xfc, 0xfa, 0xba, 0xdd, 0xc7, 0x57, 0xc1, 0x1c, 
		0x6a, 0x0c, 0x7b, 0x4b, 0xc8, 0x52, 0x54, 0x82, 0x47, 0x5d, 0xc9, 0xe8, 0x6b, 0xdb, 0x5e, 0x08,
		0xfb, 0x8d, 0x0e, 0x43, 0x37, 0x39, 0x50, 0x91, 0x7e, 0xf4, 0xe7, 0x35, 0xb8, 0x88, 0x20, 0x8b, 
		0x90, 0xe9, 0xee, 0xd5, 0xd3, 0xc3, 0xff, 0xa9, 0xae, 0x64, 0xf5, 0xac, 0x11, 0x4a, 0x76, 0x06, 
		0x18, 0x8a, 0xa3, 0xec, 0x56, 0x94, 0xdf, 0x42, 0x00, 0x22, 0xda, 0x6c, 0xb1, 0x12, 0xf2, 0xfe, 
		0xbf, 0x21, 0x1b, 0x4e, 0x9f, 0x97, 0xa6, 0x2b, 0x0b, 0xd4, 0x93, 0xc6, 0x03, 0x71, 0x14, 0x7a, 
		0x02, 0x0a, 0xc4, 0xdc, 0x36, 0x96, 0xd0, 0x09, 0x33, 0x26, 0xbc, 0x1d, 0xb6, 0xde, 0xe6, 0xe3, 
		0xeb, 0x28, 0x8c, 0x24, 0x99, 0x3f, 0xc0, 0x6f, 0xa2, 0xc2, 0xfd, 0x3c, 0x2d, 0x15, 0xf6, 0xad, 
		0x2f, 0xbd, 0x67, 0x05, 0x68, 0xa1, 0x69, 0x13, 0xca, 0x9d, 0x3a, 0x01, 0x63, 0xd7, 0x75, 0x07, 
		0x59, 0xb9, 0x46, 0xf8, 0xcd, 0x5c, 0x70, 0x95, 0xf9, 0x16, 0x45, 0xd1, 0x98, 0x79, 0x9c, 0x81, 
		0x44, 0x62, 0x6e, 0xb4, 0x34, 0xce, 0x84, 0xab, 0x29, 0x1e, 0x2a, 0x9b, 0xe2, 0x25, 0xb5, 0x87, 
		0x23, 0x3d, 0x5f, 0xaa, 0xf7, 0x9e, 0xed, 0xb3, 0xe1, 0x72, 0x7d, 0x3b, 0xb7, 0x0d, 0x51, 0x9a, 
		0x4f, 0x55, 0xf1, 0xf0, 0xe0, 0x31, 0x7f, 0xbb, 0x89, 0x5b, 0xe4, 0x78, 0x73, 0xef, 0xea, 0x92, 
		0x61, 0x41, 0x1f, 0xcc, 0xb0, 0x49, 0x85, 0x3e, 0x66, 0xaf, 0xd8, 0x2e, 0xa5, 0x10, 0xa4, 0xcf
		]
	nbit, hmsg = 64, msg.hex()
	hmsg += 'f' + hex(len(msg.hex())*4)[2:]
	hmsg += (nbit - (4*len(hmsg) % nbit)) // 4 * 'f'
	H, SBOX_M  = [], ''
	for i in range (0, len(hmsg) - 1, 2):
		tmp = hex(SBOX[int(hmsg[i:i+2], 16)])[2:]
		tmp = '0' + tmp if len(tmp) % 2 else tmp
		SBOX_M += tmp
	hmsg = SBOX_M  
	l = nbit // 4     
	H.append((int(hmsg[0:l], 16)))
	for i in range(1, len(hmsg) // l):
		plain = long_to_bytes(int(hmsg[i*l:(i+1)*l], 16))
		key = long_to_bytes(H[i-1])
		_DES = DES.new(key = key, mode = DES.MODE_OFB, IV = key)
		H.append(bytes_to_long(_DES.encrypt(plain)) ^ bytes_to_long(key))
	dgst = sha256(long_to_bytes(H[-1])).hexdigest()
	return dgst

msg = b'ETjrPXxW39mjyXXnU7ODK80xxZJxqpzVJgDIvVuzjk5ftsw1O9pQkYZsRUx1Cp4iSN'
print(len(msg))
#msg = b'iN0U5jaQAvsPSNBfqXezg4kqjV5d02uFWXS44aqdsvyoYXcK\x98\x9f\x0f\x19\xa8^\xd6\xb4'
SBOX = [
	0xbe, 0xc5, 0x0f, 0x83, 0xb2, 0x77, 0xa8, 0x40, 0x4c, 0x53, 0x65, 0xd6, 0x27, 0xa7, 0x7c, 0x48, 
	0x1a, 0x60, 0x30, 0x17, 0xf3, 0x80, 0x04, 0x74, 0xd2, 0x5a, 0x2c, 0x8e, 0xa0, 0x32, 0x38, 0xcb, 
	0xe5, 0x4d, 0x19, 0x8f, 0xd9, 0x6d, 0x86, 0x58, 0xfc, 0xfa, 0xba, 0xdd, 0xc7, 0x57, 0xc1, 0x1c, 
	0x6a, 0x0c, 0x7b, 0x4b, 0xc8, 0x52, 0x54, 0x82, 0x47, 0x5d, 0xc9, 0xe8, 0x6b, 0xdb, 0x5e, 0x08,
	0xfb, 0x8d, 0x0e, 0x43, 0x37, 0x39, 0x50, 0x91, 0x7e, 0xf4, 0xe7, 0x35, 0xb8, 0x88, 0x20, 0x8b, 
	0x90, 0xe9, 0xee, 0xd5, 0xd3, 0xc3, 0xff, 0xa9, 0xae, 0x64, 0xf5, 0xac, 0x11, 0x4a, 0x76, 0x06, 
	0x18, 0x8a, 0xa3, 0xec, 0x56, 0x94, 0xdf, 0x42, 0x00, 0x22, 0xda, 0x6c, 0xb1, 0x12, 0xf2, 0xfe, 
	0xbf, 0x21, 0x1b, 0x4e, 0x9f, 0x97, 0xa6, 0x2b, 0x0b, 0xd4, 0x93, 0xc6, 0x03, 0x71, 0x14, 0x7a, 
	0x02, 0x0a, 0xc4, 0xdc, 0x36, 0x96, 0xd0, 0x09, 0x33, 0x26, 0xbc, 0x1d, 0xb6, 0xde, 0xe6, 0xe3, 
	0xeb, 0x28, 0x8c, 0x24, 0x99, 0x3f, 0xc0, 0x6f, 0xa2, 0xc2, 0xfd, 0x3c, 0x2d, 0x15, 0xf6, 0xad, 
	0x2f, 0xbd, 0x67, 0x05, 0x68, 0xa1, 0x69, 0x13, 0xca, 0x9d, 0x3a, 0x01, 0x63, 0xd7, 0x75, 0x07, 
	0x59, 0xb9, 0x46, 0xf8, 0xcd, 0x5c, 0x70, 0x95, 0xf9, 0x16, 0x45, 0xd1, 0x98, 0x79, 0x9c, 0x81, 
	0x44, 0x62, 0x6e, 0xb4, 0x34, 0xce, 0x84, 0xab, 0x29, 0x1e, 0x2a, 0x9b, 0xe2, 0x25, 0xb5, 0x87, 
	0x23, 0x3d, 0x5f, 0xaa, 0xf7, 0x9e, 0xed, 0xb3, 0xe1, 0x72, 0x7d, 0x3b, 0xb7, 0x0d, 0x51, 0x9a, 
	0x4f, 0x55, 0xf1, 0xf0, 0xe0, 0x31, 0x7f, 0xbb, 0x89, 0x5b, 0xe4, 0x78, 0x73, 0xef, 0xea, 0x92, 
	0x61, 0x41, 0x1f, 0xcc, 0xb0, 0x49, 0x85, 0x3e, 0x66, 0xaf, 0xd8, 0x2e, 0xa5, 0x10, 0xa4, 0xcf
	]
nbit, hmsg = 64, msg.hex()
#print(hmsg)
hmsg += 'f' + hex(len(msg.hex())*4)[2:]
#print(hmsg)
hmsg += (nbit - (4*len(hmsg) % nbit)) // 4 * 'f'
print(hmsg)
H, SBOX_M  = [], ''
for i in range (0, len(hmsg) - 1, 2):
	tmp = hex(SBOX[int(hmsg[i:i+2], 16)])[2:].rjust(2,'0')
	#tmp = '0' + tmp if len(tmp) % 2 else tmp
	SBOX_M += tmp
hmsg = SBOX_M  
print(hmsg)
l = nbit // 4    
H.append((int(hmsg[0:l], 16)))

#print(hex(H[0]))
for i in range(1, len(hmsg) // l):
	plain = long_to_bytes(int(hmsg[i*l:(i+1)*l], 16))
	key = long_to_bytes(H[i-1])
	_DES = DES.new(key = key, mode = DES.MODE_OFB, IV = key)
	H.append(bytes_to_long(_DES.encrypt(plain)) ^ bytes_to_long(key))

dgst = sha256(long_to_bytes(H[-1])).hexdigest()
print('dgst',dgst)

def check(msg):
	try:
		msg = msg.decode()
	except:
		return False
	for each in msg:
		if each not in string.printable[:62]:
			return False
	return True

for _ in range(1000000):
	H1 = H[1]
	h21 = (int(hmsg[1*l:(1+1)*l], 16))


	#for _ in range(100):
	msgf = randstr(8)+msg[8:16]
	hmsgf = msgf.hex()
	Hf, SBOX_Mf  = [], ''
	for i in range (0, len(hmsgf) - 1, 2):
		tmp = hex(SBOX[int(hmsgf[i:i+2], 16)])[2:].rjust(2,'0')
		#tmp = '0' + tmp if len(tmp) % 2 else tmp
		SBOX_Mf += tmp
	hmsgf = SBOX_Mf  
	#print(hmsgf)
	l = nbit // 4    
	Hf.append((int(hmsgf[0:l], 16)))

	#print(hex(H[0]))
	for i in range(1, len(hmsgf) // l):
		plain = long_to_bytes(int(hmsgf[i*l:(i+1)*l], 16))
		#print(hmsg[i*l:(i+1)*l])
		key = long_to_bytes(Hf[i-1],8)
		_DES = DES.new(key = key, mode = DES.MODE_OFB, IV = key)
		Hf.append(bytes_to_long(_DES.encrypt(plain)) ^ bytes_to_long(key))

	H1_ = Hf[1]
	h21 = h21 ^ H1_ ^ H1

	h21 = hex(h21)[2:].rjust(16,'0')

	tmp21=''
	for i in range(0,len(h21),2):
		tmp21 += hex(SBOX.index(int(h21[i:i+2], 16)))[2:].rjust(2,'0')
	#print(tmp21)
	#print(bytes.fromhex(tmp21))
	target = bytes.fromhex(tmp21)
	if check(target):
		msg = msgf[:8]+target+msg[16:]
		print("[+]",msg)
		exit()


66
45546a725058785733396d6a7958586e55374f444b383078785a4a7871707a564a6744497656757a6a6b3566747377314f3970516b595a735255783143703469534ef210ffffffff
39d3da1b90ae0ba94b5d12dad4aeaef2c3828b3735476a0b0bf5e70b21bf93ffe74237f4a6ff9793da6c52df9f4e2b0c8b5dbfe96c64f54eeec30b0c43bfc822d5201f1acfcfcfcf
dgst 296f717f86e45b5abba7af44cc95e217dbfc439d8b9006e8541ee5b7b844360f
[+] b'kikPuOwPDsz5spcJU7ODK80xxZJxqpzVJgDIvVuzjk5ftsw1O9pQkYZsRUx1Cp4iSN'

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[root@VM-0-7-centos ~]# nc 01.cr.yp.toc.tf 37113
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  Hey hash breakers! Try to find the collision for given message and  |
|  get the flag! You have only one chance to get it in each round! :P  |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Options: 
|	[G]et the message with hash 
|	[S]end collision 
|	[Q]uit
G
| msg = b'ETjrPXxW39mjyXXnU7ODK80xxZJxqpzVJgDIvVuzjk5ftsw1O9pQkYZsRUx1Cp4iSN'
| shaim(msg) = 296f717f86e45b5abba7af44cc95e217dbfc439d8b9006e8541ee5b7b844360f
| Options: 
|	[G]et the message with hash 
|	[S]end collision 
|	[Q]uit
s
| please send message with same hash: 
WQ4J2kGsPSIjxfY8U7ODK80xxZJxqpzVJgDIvVuzjk5ftsw1O9pQkYZsRUx1Cp4iSN
| Congrats, you got the flag: CCTF{A9aiN____DES____N0T_w3AkNEs5!!}

Lagima

分值：164

考点：SymmetricGroup

challenge

You are in the road to learn some interesting cryptosystems, decrypt our cipher!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#!/usr/bin/env sage

from flag import flag

def genperm(n):
	_ = list(range(1, n + 1))
	shuffle(_)
	return _

def genlatrow(n):
	A = []
	for _ in range(n): A.append(genperm(n))
	return A

def prodlat(A, B):
	assert len(A) == len(B)
	C, G = [], SymmetricGroup(len(A))
	for _ in range(len(A)):
		g = (G(A[_]) * G(B[_])).tuple()
		C.append(list(g))
	return C

def powlat(A, n):
	assert n >= 0
	B = bin(n)[2:]
	c, R = len(B), [list(range(1, len(A) + 1)) for _ in range(len(A))]
	if n == 0: return R
	else:	
		for b in B:
			if b == '1':
				if c == 1: R = prodlat(R, A)
				else:
					T = A
					for _ in range(c - 1): T = prodlat(T, T)
					R = prodlat(R, T)
			c -= 1
	return R

G = genlatrow(313)
secret = int.from_bytes(flag.lstrip(b'CCTF{').rstrip(b'}'), 'big')
H = powlat(G, secret)

print(f'G = {G}')
print(f'H = {H}')

前面那个求底数，现在这个求指数了。

Thought

对称群的一个数学性质，之前也不知道，看题解发现的

exp

https://remyoudompheng.github.io/ctf/cryptoctf2022/lagima.html

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import json
from sage.all import SymmetricGroup, CRT

with open("output.txt") as f:
    lG = next(f)
    G = json.loads(lG.split("=")[-1])
    lH = next(f)
    H = json.loads(lH.split("=")[-1])

Sn = SymmetricGroup(313)
g = [Sn(x) for x in G]
h = [Sn(x) for x in H]

rems = {}
for i, gi in enumerate(g):
    for c in gi.cycle_tuples():
        l = len(c)
        k = c.index(h[i](c[0]))
        if l in rems:
            assert rems[l] == k
        else:
            rems[l] = k
c = CRT(list(rems.values()), list(rems.keys()))
print(int(c).to_bytes(64, "big").lstrip(b'\0'))

result

1
b'3lGam4L_eNcR!p710n_4nD_L4T!n_5QuarS3!'

Versace

分值：226

考点：大整数分解

challenge

What is most important when we have prime numbers? Answer and decrypt the message!

Note: The output file has changed, Please download again!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#!/usr/bin/env python3
# In the name of Allah

from Crypto.Util.number import *
from flag import flag

def keygen(n):
	e = 65537
	x, y = [getRandomRange(2, n - 2) for _ in '01']
	fi = pow(5, x, n)
	th = pow(13, y, n)
	return (n, e, fi, th)

def encrypt(m, pubkey):
	n, e, fi, th = pubkey
	k, u, v = [getRandomRange(2, n - 2) for _ in '012']
	c_1 = pow(k, e, n)
	c_2 = pow(5, u, n)
	c_3 = pow(13, v, n)
	c_4 = pow(fi, u, n) * pow(th, v, n) * pow(k + 1, e, n) * m % n
	return c_1, c_2, c_3, c_4


n = 141886649864474336567180245736091175577519141092893110664440298696325928109107819365023509727482657156444454196974621121317731892910779276975799862237645015028934626195549529415068518701179353407407170273107294065819774663163018151369555922179926003735413019069305586784817562889650637936781439564028325920769
pubkey = keygen(n)
msg = bytes_to_long(flag.encode('utf-8'))
enc = encrypt(msg, pubkey)

print(f'pubkey = {pubkey}')
print(f'enc = {enc}')

pubkey = (141886649864474336567180245736091175577519141092893110664440298696325928109107819365023509727482657156444454196974621121317731892910779276975799862237645015028934626195549529415068518701179353407407170273107294065819774663163018151369555922179926003735413019069305586784817562889650637936781439564028325920769, 65537, 125494383162828289973475117066203219587304356806057400173045477137700391356840397636206107925460433939119412469184723408274805651096828270461235114589209044543108910295997506041345432448035371092981112305692014036117962906342882215492784319467728201344342591126197621795974549431806828947671232171059809967991, 138257736445723754207239869344459794807808248188757696052272858978544083465381926995900887162870612185045399616892685750962667762789508194359878372465943702647287813020223160406789982302692329883577043521781397505345137392777694159916452699296748509096494301465498192136911589776144421856343483031920756519249)
enc = (88920444409754899592335110119456825172544580816901497880270628553955508488170483498726344301421934007876515783471747430111559265733377611608113080609941423596790625452564403457107243481310552344096683637970851198148957553062631972064855184560312748315536290880767375156429548232884895308088306625307674645678, 45539956581550314230977168288877082058214432324397034618326297663129864608739856352261029083496409133620455599376139981575342903237304167908534019438874239934645347320209162850653298515960349717851268830205737252263548268549179642907155075129172651815656517165432021020317138111104384072600486843574535899860, 69849817078368866947686316374564245958824276178721440086311727765763093314086243149277327430285562537315291446874425715021031882041090977200029684675392021083309757246079110723453995717856469919242618068208424495615283285085190255592463862108516827540775850882615540406750734639040903336048095547788528187976, 20285007564778647051596518902857046010716548094264173639037549746086538656814534621919993169453446815272789643882592631536755194356753848872566348635207131520597253599540337542405837637606323276917410384296602682043902830628022440639028040137219164743287397377174047728489836106561656239657061612908104843401)

Thought

想要解密肯定是要先算出 $fi^u \cdot th^v \cdot (k+1)^e$

题目给出了 $n,e,fi,th,k^e,5^u,13^v$

那么我们需要解出 $k,u,v$

其中 $k$ 要大整数分解

$u,v$ 要解离散对数

只要能够分解这个 $n$ 就好了。

发现使用 Williams p+1 可以给这 $n$ 秒分了，

然后 $p-1 = 2^{18} \cdot 3^{30} \cdot 7^{53} \cdot 11^{12}$，好解离散对数

但是另一半似乎有点难搞，

chao，多运行几次，会发现结果不一样，原来有三个因子，都是这样子的形式。

分解之后分别在 $p,q,r$ 求离散对数，求 $m$，最后给 $m$ 走一个 crt 就好了。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
from gmpy2 import iroot,gcd
from tqdm import tqdm
import random
from math import log
prime = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,997]


def Lucas_pow(P, R):
	A, B = P, 2
	R = bin(R)[3:]
	for i in R:
		if int(i) == 1:
			A, B = (P * A**2 - A * B - P) % n, (A**2 - 2) % n
		else:
			A, B = (A**2 - 2) % n, (A * B - P) % n
	return gcd(A - 2, n)

def Williams_p_1(n):
	print("[+]Trying William's p+1...\n")
	R = 1
	B = int(iroot(n, 2)[0])
	B = log(B)
	for pi in prime:
		for i in range(int(B/log(pi))):
			R *= pi
	while True:
		P = random.randint(2, int(B))
		p = Lucas_pow(P, R)
		if p > 1 and p < n:
			q = n // p
			print("p: ", p)
			print("q: ", q)
			return p,q

n = 141886649864474336567180245736091175577519141092893110664440298696325928109107819365023509727482657156444454196974621121317731892910779276975799862237645015028934626195549529415068518701179353407407170273107294065819774663163018151369555922179926003735413019069305586784817562889650637936781439564028325920769

# run this function servral times we get
Williams_p_1(n)
# q = 104492689192892408108975038373966852967734827395344990285038653889732962680833
# p = 12735676857401163601385118447483795668229644118624917660231942016044435957817541173149617917604011645058841872384142319678290750015804888147769138207522817
# r = 106618752612001652530923691512073519044983443846656721126867402977583225110529

# sage
pubkey = (141886649864474336567180245736091175577519141092893110664440298696325928109107819365023509727482657156444454196974621121317731892910779276975799862237645015028934626195549529415068518701179353407407170273107294065819774663163018151369555922179926003735413019069305586784817562889650637936781439564028325920769, 65537, 125494383162828289973475117066203219587304356806057400173045477137700391356840397636206107925460433939119412469184723408274805651096828270461235114589209044543108910295997506041345432448035371092981112305692014036117962906342882215492784319467728201344342591126197621795974549431806828947671232171059809967991, 138257736445723754207239869344459794807808248188757696052272858978544083465381926995900887162870612185045399616892685750962667762789508194359878372465943702647287813020223160406789982302692329883577043521781397505345137392777694159916452699296748509096494301465498192136911589776144421856343483031920756519249)
enc = (88920444409754899592335110119456825172544580816901497880270628553955508488170483498726344301421934007876515783471747430111559265733377611608113080609941423596790625452564403457107243481310552344096683637970851198148957553062631972064855184560312748315536290880767375156429548232884895308088306625307674645678, 45539956581550314230977168288877082058214432324397034618326297663129864608739856352261029083496409133620455599376139981575342903237304167908534019438874239934645347320209162850653298515960349717851268830205737252263548268549179642907155075129172651815656517165432021020317138111104384072600486843574535899860, 69849817078368866947686316374564245958824276178721440086311727765763093314086243149277327430285562537315291446874425715021031882041090977200029684675392021083309757246079110723453995717856469919242618068208424495615283285085190255592463862108516827540775850882615540406750734639040903336048095547788528187976, 20285007564778647051596518902857046010716548094264173639037549746086538656814534621919993169453446815272789643882592631536755194356753848872566348635207131520597253599540337542405837637606323276917410384296602682043902830628022440639028040137219164743287397377174047728489836106561656239657061612908104843401)

n, e, fi, th = pubkey
c_1, c_2, c_3, c_4 = enc
q = 104492689192892408108975038373966852967734827395344990285038653889732962680833
p = 12735676857401163601385118447483795668229644118624917660231942016044435957817541173149617917604011645058841872384142319678290750015804888147769138207522817
r = 106618752612001652530923691512073519044983443846656721126867402977583225110529

from Crypto.Util.number import *
phi = (p-1)*(q-1)*(r-1)
d = inverse(e,phi)
k = pow(c_1,d,n)
up = discrete_log(Mod(c_2,p),Mod(5,p))
uq = discrete_log(Mod(c_2,q),Mod(5,q))
ur = discrete_log(Mod(c_2,r),Mod(5,r))


vp = discrete_log(Mod(c_3,p),Mod(13,p))
vq = discrete_log(Mod(c_3,q),Mod(13,q))
vr = discrete_log(Mod(c_3,r),Mod(13,r))


fxxkp = pow(fi, up, p) * pow(th, vp, p) * pow(k + 1, e, p) % p
fxxkq = pow(fi, uq, q) * pow(th, vq, q) * pow(k + 1, e, q) % q
fxxkr = pow(fi, ur, r) * pow(th, vr, r) * pow(k + 1, e, r) % r
mp = c_4 * inverse(int(fxxkp),int(p)) % p
mq = c_4 * inverse(int(fxxkq),int(q)) % q
mr = c_4 * inverse(int(fxxkr),int(r)) % r
print(long_to_bytes(crt([mp,mq,mr],[p,q,r])))

result

1
b'CCTF{8As3d_oN_f4c70r1n9_4nD_d15cr3tE_lOgaRiThM!}'

hard

GSDP

分值：164

考点：

challenge

A very modern cryptography! Break it harder!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#!/usr/bin/env sage

from Crypto.Util.number import *
from flag import flag

def hash_base(m):
	m = M(m)
	_M = M(zero_matrix(d))
	for i in range(d):
		for j in range(d):
			_M[i, j] = pow(2, m[i, j], n)
	return M(_M)

def rand_poly(deg):
	P = PolynomialRing(Zn, 'x')
	x = P.gen()
	f = 0
	for _ in range(deg):
		f += randint(0, deg**2)*x**(_)
	return f

def matrox(a, b):
	a, b = M(a), M(b)
	R = zero_matrix(d)
	for i in range(d):
		for j in range(d):
			R[i, j] = int(a[i, j]) ^^ int(b[i, j])
	return M(R)

flag = flag.lstrip('CCTF{').rstrip('}')
assert len(flag) == 25
msg = [[ord(flag[j]) for j in range(5*i, 5*i + 5)] for i in range(5)]

nbit = 72
p, q = [getPrime(nbit) for _ in '01']
n = p * q

d, Zn = 5, Zmod(n)
M = MatrixSpace(Zn, d, d)

m = hash_base(msg)
u, v = [randint(2, 14) for _ in '01']
P = PolynomialRing(Zn, 'x')
x = P.gen()
f, h = rand_poly(d), x**d + x + 1
r, s = [random_matrix(Zn, d) for _ in '01']
y = f(r) ** u * s * f(r) ** v
c_1 = h(r) ** u * s * h(r) ** v
c_2 = matrox(hash_base(h(r) ** u * y * h(r) ** v), m)

print(f'n = {n}')
print(f'r = {r}')
print(f's = {s}')
print(f'y = {y}')
print(f'c_1 = {c_1}')
print(f'c_2 = {c_2}')

Thought

u，v那么小，，爆

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
n=20474248118672564431085568112167867588651829
r=[[2168977325369444782802512809005167009163457,9637731563002649997560875900298785659999735,11402741982195550777990817093767890991834736,6248261665690503242396669505673833765541530,18383713927317640760514600671318653784954042],
[16744026390724915738262959513570982580233867,10819123318870588054961801715028528659245735,5382293825969147064471127752184942873958882,2344559383975384575566938072263260707083674,6107831242377773278696901510341268870768483],
[13913478639322625565461944432421523802028490,1657756157808133991943366467693421012417454,20077078978711296540965234618986335826824167,15787724170325517021960596569296223410283963,11311327970428371404045885802092772454814312],
[6961572103900078883590821780051797472394845,9455345930492634517894541442153982197931104,7188007809979291502164073459871201264229019,5450777010613496799286069470550372888274079,19294083677962489844799387987438241606854764],
[2085952337131731679161648956407072286901978,6312527395255217479599228946227018949620025,3768572167307432043022080651953496439648407,12149358492352082063390352013944276402659624,1238053480843820309901822772557963596458725]]
s=[[14359986778171934757328112351570087412922923,11851267097835964101770194163721259897123880,12595767519284390452196370829927812771980581,206471849033914539608937494910010443534631,16748276256578102130941428769109053956841543],
[17260552917456245674154511124533873366489719,6705751087806309384311406617121931614484164,17060390771834209118913353599009244296476485,14200001344699610276445944574627003822066232,11014902955514050741738009264685742116160993],
[6574547665819712697427953197398960761636762,12380657135986764418898027400335749204149860,20268210493845979828493975027685347139394991,18542561637456865344299035395313783209218383,7517573123535289654812496192079398350464721],
[11797258068553520501845550128339899816126913,18396577268206658268808323909560870783161039,5490905135614309369346662799065239256309022,14271245849005639472351475697722779937695903,4543895191969014210971676462965142633095929],
[8211670484406041965410550067328494865731128,9385233048164928123059801337014436991987865,2095213218314387589455876832673480152942740,13404162072797239424739266925419641170015472,6893572325245832032339890201821364839102869]]
y=[[9455266042843307825749316910810796871873373,15333106063741475447799261101208428669252581,17507977101165165875868259123812011424101505,18840713703683969794184618879025658583771001,8194677825423260832777930195809869229371863],
[12501728660245911874452737460699597975974127,19510243647017562462989706821025083261970404,16201393977361396153964696776216973010001356,9663056411865435751212414658633217623172749,3239680106699734686590526219042751814995824],
[3712586611180063604215543952289707697324027,14733212399197986119485181728946640781107458,2840139099323763287710523315368925837277792,13720228569300291500610175158110171144774084,6108815350519225911945135207538331156078296],
[7943973119701029382921917301472306070824581,2869347305630973901685036806460889911095637,10842022254827356928486285947954965977783240,20363982398752260203093070660357855892929807,3232527006736169029584220678644241677651188],
[18741615057330867264302735709730246936126331,7207581826003452274777064725926668618294351,12235279908760679864964056098862023499484670,11395481161377031878998588680860748310228740,14691306415490831547905993706341909177907668]]
c_1=[[14520715136678131886650886394655992310739740,5133803346119603685589690243318329447613811,8631069083165564771821540186676532972101042,11371460936058753234877719062830204068473293,4675643908977844081807119750891783452511801],
[10758446634943798177756512241470807154028028,230322671654482905785761279475308992164431,19859272618066856343509476253828743509021381,10790059806866303289733349155468067057434048,7937553273189724162746367232714449171157875],
[12713707768421115203045631708468778038780988,6562443329388128558909111073920129986165358,8629397281530840800788762372728359271085200,3497280351202001940823865223283895540070188,16324531747558707671873605114378727152000738],
[17664302494165645750553234381674396726461155,11329821313213471881023356172069963076578223,17420708004114170496283987639981918922808988,4025301508682028642713745479550070150287792,13516995862604528976910352157951268294502659],
[13197381126644223748863331681581035046689048,18134793368131211547774737770284104243998582,3304296884612368960093061281547555357926671,17654343876553302292700074689920978613390384,19965538184282119398237005639724114717256368]]
c_2=[[7467508370111086497875591641000575993385737,436730215933598480688770862716304678927061,16388674389038775692052384536812272916184391,1544929917235051621830007372321346311674993,20266847919326089072814025756784393554435095],
[8525400103718228392870804572553779730855209,6910832586632574200490719455813022347001485,17879158289938108082881632425571195671456277,10773037736439027909506921110474733019517450,6673285991052846421739430171898388311111793],
[9870026505859633975247413380429542368374340,3599087047295232637660012477486366289652163,9771908525081529326761727267151928531319243,19335625816265272435673905591707160166566864,15219307175745538685718076680399058971932192],
[7121095235650179073589022177762837236165521,10051305836914620675997951100253778882475518,14120877609199150307731361282669945615365363,3064435253345055470095756982744706296418025,126078528977194834765813221549264972548412],
[18926039657432874696099563502261812215936524,14159758827498805644159739654028640645658626,4643672049840979864316682883185591331924981,20293416534996028081504808704845564317319704,5806383537343185356941724671128323142478351]]



def hash_base(m):
	m = M(m)
	_M = M(zero_matrix(d))
	for i in range(d):
		for j in range(d):
			_M[i, j] = pow(2, m[i, j], n)
	return M(_M)

def rand_poly(deg):
	P = PolynomialRing(Zn, 'x')
	x = P.gen()
	f = 0
	for _ in range(deg):
		f += randint(0, deg**2)*x**(_)
	return f

def matrox(a, b):
	a, b = M(a), M(b)
	R = zero_matrix(d)
	for i in range(d):
		for j in range(d):
			R[i, j] = int(a[i, j]) ^^ int(b[i, j])
	return M(R)

d, Zn = 5, Zmod(n)
r = matrix(Zn,r)
c_1 = matrix(Zn,c_1)
s = matrix(Zn,s)
for u in range(2,14):
    for v in range(2,14):
        if c_1 == h(r) ** u * s * h(r) ** v:
            print(u,v)



M = MatrixSpace(Zn, d, d)
u = 11
v = 12
c_2 = matrix(Zmod(n),c_2)
y = matrix(Zmod(n),y)
m = matrox(hash_base(h(r) ** u * y * h(r) ** v), c_2)
flag=""
for each in m:
	for i in each:
		flag+=chr(discrete_log(Mod(i,n),Mod(2,n)))
print(flag)

result

1
PKCS_N0n_cOmMu74T!v3_rIn9

Persian cat

分值：247

考点：block cipher

challenge

Persian cat

Can you check this crypto system and let us know the message? You will find this crypto system very adroit!

1
2
3
4
nc 03.cr.yp.toc.tf 11173
nc 07.cr.yp.toc.tf 11173
nc 05.cr.yp.toc.tf 11173
nc 02.cr.yp.toc.tf 11173
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
#!/usr/bin/env python3

import random, sys
#from secret import skey, flag
flag = "CCTF"*10
skey = b"A"*20
Omega = [
		0x4e, 0x96, 0xfd, 0x7d, 0x8d, 0xf6, 0xdb, 0x33, 0x1e, 0x16, 0x9b, 0x6a, 0xe2, 0xc9, 0xa9, 0xe0, 
		0x34, 0xe6, 0x86, 0xd6, 0x52, 0x02, 0x25, 0x1f, 0x23, 0xdf, 0xd5, 0x12, 0x45, 0x6b, 0x6f, 0x4d, 
		0x31, 0x77, 0x09, 0xbf, 0x93, 0xca, 0x4b, 0xef, 0xee, 0x7c, 0x53, 0x1a, 0xc8, 0xea, 0x9d, 0xda, 
		0x32, 0xa4, 0x11, 0x7b, 0xd8, 0x3f, 0x13, 0x57, 0x75, 0xcb, 0x37, 0x9a, 0x83, 0xa5, 0x3e, 0xd3, 
		0x4a, 0x1d, 0x29, 0xb9, 0x18, 0x27, 0x2d, 0x0f, 0x15, 0x0d, 0x66, 0xae, 0xf5, 0xfa, 0x08, 0x9f, 
		0xc6, 0x55, 0xa0, 0xb7, 0x28, 0x0e, 0xf4, 0x01, 0x04, 0x46, 0xf9, 0x39, 0xe3, 0x7f, 0x5e, 0x61, 
		0x40, 0x26, 0xec, 0xb6, 0x14, 0xf0, 0x59, 0x50, 0xcf, 0x3a, 0x8b, 0x43, 0xaf, 0x10, 0xe5, 0xe8, 
		0x03, 0xbd, 0x51, 0xa7, 0x1c, 0x8e, 0x7a, 0x98, 0x3c, 0xeb, 0xac, 0x54, 0x84, 0xf7, 0x62, 0x88, 
		0x64, 0xa8, 0xbb, 0xab, 0xe1, 0x95, 0x94, 0x41, 0x2a, 0x60, 0x30, 0xcc, 0x48, 0xd2, 0x89, 0xb2, 
		0x65, 0x76, 0x0a, 0xb8, 0x56, 0x4f, 0xc3, 0x87, 0xdd, 0x4c, 0xc2, 0xd4, 0x82, 0x35, 0x90, 0xa2, 
		0x5f, 0xad, 0x19, 0x74, 0x73, 0xd0, 0x24, 0x69, 0x20, 0x07, 0xdc, 0x1b, 0x44, 0x58, 0xff, 0x5a, 
		0x6c, 0xf2, 0xfb, 0x8c, 0x79, 0x97, 0xa6, 0x22, 0xb4, 0x7e, 0x5b, 0x17, 0x2f, 0x91, 0x71, 0xfe, 
		0x38, 0xa3, 0x05, 0xb1, 0xba, 0x99, 0xd9, 0xf1, 0x21, 0x5c, 0x67, 0x6d, 0xde, 0xaa, 0xc7, 0x8f, 
		0x81, 0x0b, 0xb0, 0xbc, 0x0c, 0xcd, 0x63, 0xc1, 0xfc, 0xc0, 0x42, 0x78, 0xc5, 0x8a, 0x06, 0x3d, 
		0x2e, 0x9e, 0xa1, 0x80, 0xb3, 0xf8, 0xe9, 0x68, 0xd1, 0x36, 0x70, 0x49, 0xc4, 0xd7, 0x2c, 0x6e, 
		0xe7, 0xb5, 0xbe, 0x92, 0xce, 0xed, 0xf3, 0x9c, 0xe4, 0x3b, 0x47, 0x2b, 0x85, 0x5d, 0x72, 0x01
		]

def padding(msg):
	if len(msg) % 32 != 0:
		extra = '*' * (32 - len(msg) % 32)
		return msg + extra
	else:
		return msg

def keygen(u, v):
	return [a ^ b for a, b in zip(u, v)][:20]

def roadrunner(table, roadrunner_wile, lili, lilibeth, omega):
	for z in range(16):
		roadrunner_wile[z] = (((omega[table[lili[z][0]]] | omega[table[lili[z][1]]]) +
			(omega[table[lili[z][2]]] | omega[table[lili[z][3]]])) ^ ((omega[table[lili[z][4]]] +
			omega[table[lili[z][5]]]) + (omega[table[lili[z][6]]] ^ omega[table[lili[z][7]]]))) % 256
		roadrunner_wile[z] = (roadrunner_wile[z] + (((~omega[table[lili[z][8]]] ^ omega[table[lili[z][9]]]) +
			(omega[table[lili[z][10]]] & ~omega[table[lili[z][11]]])) ^ ((omega[table[lili[z][12]]] ^ 
			~omega[table[lili[z][13]]]) + (omega[table[lili[z][14]]] ^ omega[table[lili[z][15]]])))) % 256
		roadrunner_wile[z] = (roadrunner_wile[z] + lilibeth[roadrunner_wile[z]] + lilibeth[z]) % 256
	return roadrunner_wile

def roadrunner_init(table, roadrunner_wile, lili, lilibeth, omega):
	SBOX = [
		[10, 11, 4, 5, 15, 0, 2, 3, 1, 9, 14, 6, 7, 12, 8, 13], 
		[1, 11, 13, 2, 0, 7, 3, 8, 14, 4, 6, 15, 5, 10, 12, 9], 
		[1, 9, 0, 4, 11, 5, 2, 8, 15, 7, 3, 6, 10, 14, 13, 12], 
		[5, 0, 9, 8, 3, 10, 12, 4, 1, 6, 7, 11, 15, 14, 2, 13], 
		[10, 6, 13, 3, 2, 11, 12, 14, 5, 9, 4, 1, 0, 8, 15, 7], 
		[15, 6, 1, 10, 7, 13, 14, 8, 3, 12, 0, 5, 2, 9, 4, 11], 
		[13, 7, 9, 5, 14, 12, 8, 15, 6, 0, 10, 4, 3, 11, 2, 1], 
		[13, 15, 8, 10, 6, 11, 9, 7, 12, 2, 3, 4, 14, 0, 5, 1], 
		[11, 3, 14, 7, 4, 8, 12, 2, 13, 0, 6, 1, 9, 10, 5, 15], 
		[2, 3, 14, 9, 11, 5, 15, 0, 4, 7, 1, 6, 12, 13, 8, 10], 
		[13, 3, 14, 1, 10, 0, 6, 5, 7, 2, 4, 9, 12, 8, 11, 15], 
		[15, 7, 4, 12, 14, 2, 9, 6, 3, 1, 13, 5, 0, 8, 11, 10], 
		[10, 7, 5, 14, 6, 2, 15, 1, 8, 11, 12, 9, 0, 3, 4, 13], 
		[1, 5, 0, 4, 6, 9, 11, 12, 3, 14, 7, 2, 15, 8, 13, 10], 
		[14, 9, 11, 2, 10, 4, 3, 0, 5, 8, 6, 15, 1, 12, 13, 7], 
		[11, 13, 6, 2, 0, 9, 3, 12, 1, 8, 7, 15, 4, 5, 10, 14]
		]
	for z in range(16):
		roadrunner_wile[z] = (((omega[table[SBOX[z][0]]] | omega[table[SBOX[z][1]]]) +
			(omega[table[SBOX[z][2]]] | omega[table[SBOX[z][3]]])) ^ ((omega[table[SBOX[z][4]]] +
			omega[table[SBOX[z][5]]]) + ( omega[table[SBOX[z][6]]] ^ omega[table[SBOX[z][7]]]))) % 256
		roadrunner_wile[z] = (roadrunner_wile[z] + (((~omega[table[SBOX[z][8]]] ^ omega[table[SBOX[z][9]]]) + 
			(omega[table[SBOX[z][10]]] & ~omega[table[SBOX[z][11]]])) ^ ((omega[table[SBOX[z][12]]] ^ 
			~omega[table[SBOX[z][13]]]) + (omega[table[SBOX[z][14]]] ^ omega[table[SBOX[z][15]]])))) % 256
	return roadrunner_wile

def circle_it_out(msg, ruler, roadrunner_wile, lili, lilibeth, enc, l, r, omega):
	for i in range(16):
		l[0][i] = msg[i]
		r[0][i] = msg[i+16]
	for i in range(1, ruler):
		roadrunner_wile = roadrunner(r[i-1], roadrunner_wile, lili, lilibeth, omega)
		for y in range(16):
			l[i][y] = r[i-1][y]
			r[i][y] = (l[i-1][y] ^ roadrunner_wile[y])%256
	for i in range(16):
		enc[i+16] = l[ruler-1][i]%256
		enc[i] = r[ruler-1][i]%256
	return roadrunner_wile, enc, l, r

def circle_it_out_init(msg, ruler, roadrunner_wile, lili, lilibeth, enc, l, r, omega):
	for i in range(16):
		l[0][i] = msg[i]
		r[0][i] = msg[i+16]
	for i in range(1,ruler):
		roadrunner_wile = roadrunner_init(r[i-1], roadrunner_wile, lili, lilibeth, omega)
		for y in range(16):
			l[i][y] = r[i-1][y]
			r[i][y] = (l[i-1][y] ^ roadrunner_wile[y])%256
	for i in range(16):
		enc[i] = l[ruler-1][i]%256
		enc[i+16] = r[ruler-1][i]%256
	return roadrunner_wile, enc, l, r

def persian_init(key, roadrunner_wile, lili, lilibeth, enc, l, r, omega, Omega):
	stkey = [88, 20, 64, 181, 251, 167, 69, 243, 205, 166, 110, 65, 90, 176, 229, 46, 206, 104, 15, 19, 49, 101, 3, 223, 221, 231, 232, 43, 62, 193, 80, 228]
	for compt in range(256):
		omega[compt] = (Omega[compt]^key[compt%20]) % 256
	for w in range(4):
		roadrunner_wile, enc, l, r = circle_it_out_init(stkey, 32, roadrunner_wile, lili, lilibeth, enc, l, r, omega);
		for compt in range(256):
			omega[compt] = (omega[compt]^enc[compt%32])%256
		for compt in range(32):
			stkey[compt] = enc[compt]
	for compt in range(16):
		err = 0
		ix = 0
		while ix < 16:
			roadrunner_wile, enc, l, r = circle_it_out_init(enc, 4, roadrunner_wile, lili, lilibeth, enc, l, r, omega)
			x = 0
			while x < ix:
				if lili[compt][x] == (enc[7]%16):
					x = ix
					err = 1
					roadrunner_wile, enc, l, r = circle_it_out_init(enc, 4, roadrunner_wile, lili, lilibeth, enc, l, r, omega)
				else: x += 1
			if err == 0: lili[compt][ix] = enc[7]%16
			else:
				err = 0;
				ix = ix-1;
			ix += 1
	err = 0 
	ix = 0
	while ix < 256:
		roadrunner_wile, enc, l, r = circle_it_out_init(enc, 4, roadrunner_wile, lili, lilibeth, enc, l, r, omega)
		x = 0
		while x < ix:
			if lilibeth[x] == ( enc[7]%256):
				x  = ix 
				err = 1
				roadrunner_wile, enc, l, r = circle_it_out_init(enc, 4, roadrunner_wile, lili, lilibeth, enc, l, r, omega)
			else:	
				x += 1
		if err == 0: lilibeth[ix]=enc[7]%256
		else:
			err = 0;
			ix = ix-1;
		ix += 1
	for compt in range(256):
		omega[compt] = (omega[compt] ^ key[compt%20])%256	
	for w in range(4):
		roadrunner_wile, enc, l, r = circle_it_out_init(stkey, 32, roadrunner_wile, lili, lilibeth, enc, l, r, omega)
		for compt in range(256):
			omega[compt] = (omega[compt] ^ enc[compt%32])%256
		for compt in range(32):
			stkey[compt] = enc[compt]
	return roadrunner_wile, lili, lilibeth, enc, l, r, omega

def encrypt_iginition(msg, key):
	roadrunner_wile = [0 for x in range(16)]
	lili = [[0 for x in range(16)] for y in range(256)] 
	lilibeth, omega = [[0 for x in range(256)] for _ in '01']
	enc = [0 for x in range(32)]
	l, r = [[[0 for x in range(16)] for y in range(32)] for _ in '01'] 
	roadrunner_wile, lili, lilibeth, enc, l, r, omega = persian_init(key, roadrunner_wile, lili, lilibeth, enc, l, r, omega, Omega)
	roadrunner_wile, enc, l, r = circle_it_out(msg, 6, roadrunner_wile, lili, lilibeth, enc, l, r, omega)
	return enc

def encrypt(msg, key):
	msg = padding(msg)
	blocks = [msg[i*32:i*32+32] for i in range(len(msg) // 32)]
	ciphers = []
	enc = encrypt_iginition([ord(item) for item in blocks[0]], key)
	ciphers.append(enc)
	for i in range(len(blocks)-1):
		enc = encrypt_iginition([ord(item) for item in blocks[i+1]], keygen([ord(item) for item in blocks[i]], ciphers[i]))
		ciphers.append(enc)
	return "".join("".join(str(format(i, "02x")) for i in item) for item in ciphers)

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "|"
	pr(border*72)
	pr(border, "Hello guys! This challenge is about breaking a symmetric cipher that", border)
	pr(border, "we have implemented here, your mission is find the flag, have fun :)", border)
	pr(border*72)

	while True:
		pr("| Options: \n|\t[E]encrypt message \n|\t[Q]uit")
		ans = sc().lower()
		if ans == 'e':
			pr(border, 'please send you message: ')
			msg = sc()
			enc = encrypt(msg + flag, skey)
			pr(border, f'enc = {enc}')
		elif ans == 'q': die("Quitting ...")
		else: die("Bye bye ...")

if __name__ == '__main__':
	main()

Thought

代码过于长了，加密的内容也好麻烦好绕，看着让人头大。不过细看一下，似乎也就是一个纸老虎

注意到 encrypt 函数，

1
2
3
4
5
6
7
8
9
10
def encrypt(msg, key):
	msg = padding(msg)
	blocks = [msg[i*32:i*32+32] for i in range(len(msg) // 32)]
	ciphers = []
	enc = encrypt_iginition([ord(item) for item in blocks[0]], key)
	ciphers.append(enc)
	for i in range(len(blocks)-1):
		enc = encrypt_iginition([ord(item) for item in blocks[i+1]], keygen([ord(item) for item in blocks[i]], ciphers[i]))
		ciphers.append(enc)
	return "".join("".join(str(format(i, "02x")) for i in item) for item in ciphers)

是块加密，一次加密32个比特，加密公式为

$c_0 = Enc(m_0,k)$

$c_i = Enc(m_i,g(m_{i-1}) \oplus c_{i-1})$

有那么有点 $CBC$ 模式的味道。

注意到我们在交互的时候，传入 $msg$，会返回 $c = encrypt(msg+flag,k)$

那么进行一手逐字节爆破就可以了吧。第一次传入 “A” * 31，那么第一组就会是 “A”*31 + flag[0] 的密文，我们爆破这个字节就好了。以此类推可以获取flag的前32个字节。那后面的字节怎么办呢？

那我们可以第一次传入 “A” * 64，看第二组的密文来开始爆，这样能爆出 $flag$ 的64个字节，以此类推。。。（怪不得给了这么多地址）

但是春哥顶啊，直接就是对波斯猫的一个硬撸。

exp

NLCS x

分值：375

考点：LFSR、PolynomialRing

challenge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#!/usr/bin/env sage

from Crypto.Util.number import *
from flag import flag

def Eval_Poly(feedabck , States):
	next_s = 0
	for i in range(len(feedabck) - 1):
		if feedabck[i]:
			next_s = next_s + States[i]
	return next_s


flag = flag.lstrip('CCTF{').rstrip('}')
m = bytes_to_long(flag.encode('utf-8'))
IS, l = '0' + bin(m)[2:], len(bin(m)[2:]) + 1

registers= ['s' + str(i) for i in range(l)]
A = BooleanPolynomialRing(names = registers, order = TermOrder("lex"))

P = PolynomialRing(ZZ, 'x')
x, FF = P.gen(), GF(2)

IS = [FF(_) for _ in IS]
f = x^64 + x^33 + x^30 + x^26 + x^25 + x^24 + x^23 + x^22 + x^21 + x^20 + x^18 + x^13 + x^12 + x^11 + x^10 + x^7 + x^5 + x^4 + x^2 + x + 1
LFSR = LFSRCryptosystem(FF)

Encryptor = LFSR((f,IS))

ins = Encryptor.initial_state()
poly = [FF(_) for _ in f.list()]
SIZE = 2 ** (l // 4)
IKEY = lfsr_sequence(poly, IS, SIZE)
KEY = ''
for i in range(SIZE - l):
	S = [FF(t) for t in IKEY[i:i + l]]
	KEY += str(
		S[0] + S[12] + S[62] + S[18] + S[36] + 
		S[2]*S[8] + 
		S[34]*S[20] +
		S[27]*S[60] +
		S[31]*S[34] +
		S[63]*S[48] +
		S[50]*S[15] +
		S[25]*S[49] +
		S[49]*S[7]  +
		S[13]*S[61]*S[10] +
		S[32]*S[37]*S[29] +
		S[9]*S[6]*S[42] +
		S[59]*S[26]*S[55] +
		S[42]*S[41]*S[29] +
		S[58]*S[24]*S[28]
		)

enc = long_to_bytes(int(KEY, 2))
f = open('flag.enc', 'wb')
f.write(enc)
f.close()

是没有解出来的题目，那么，就留给大佬了~

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com

赏

文章标题:2022 CryptoCTF

文章字数:16.8k

本文作者:Van1sh

发布时间:2022-09-14, 17:16:00

最后更新:2023-03-07, 18:35:03

原始链接:http://jayxv.github.io/2022/09/14/2022 cryptoctf/

版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

©2020 Van1sh

Built with Hexo and 3-hexo theme

目录
×

喜欢就点赞,疼爱就打赏